Hier erfährst du, wie du mit den Winkelfunktionen mathematische Probleme aus dem Alltag lösen kannst. Winkelfunktionen und Seitenverhältnisse Lösen von Anwendungsaufgaben Schritt für Schritt Vermessungen mit dem Theodolit Winkelfunktionen und Seitenverhältnisse Je nach Wahl des Winkels bekommen die Seiten im rechtwinkligen Dreieck „neue Namen“. Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen […]
Trigonometrie
Hier erfährst du, wie du mit den Winkelfunktionen unzugängliche Streckenlängen und Winkel in Figuren und Körpern berechnen kannst. Winkelfunktionen und Seitenverhältnisse Lösen von Anwendungsaufgaben Schritt für Schritt Winkelfunktionen und Seitenverhältnisse Je nach Wahl des Winkels bekommen die Seiten im rechtwinkligen Dreieck „neue Namen“. Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, […]
Hier erfährst du, wie du mit Hilfe der Winkelfunktionen Sinus, Kosinus und Tangens Seitenlängen und Winkelgrößen am rechtwinkligen Dreieck berechnen kannst und wie du dabei den Taschenrechner richtig benutzt. Winkelfunktionen und Seitenverhältnisse Benutzung des Taschenrechners Berechnung von Winkeln und Seitenlängen Winkelfunktionen und Seitenverhältnisse Da rechtwinklige Dreiecke mit gleich großen Winkeln ähnlich zueinander sind, sind die […]
Hier erfährst du, wie du mit dem Kosinussatz Seitenlängen und Winkel an beliebigen Dreiecken berechnen kannst Der Kosinussatz Seitenlänge berechnen Winkel berechnen Der Kosinussatz Seitenlänge berechnen Mit dem Kosinussatz kannst du aus den Längen zweier Seiten und dem eingeschlossenen Winkel (sws) die Länge der dritten Seite berechnen. Winkel berechnen Mit dem Kosinussatz kannst du aus […]
Hier erfährst du, wie du mit dem Sinussatz Seitenlängen und Winkel in beliebigen Dreiecken berechnen kannst. Der Sinussatz Seitenlängen berechnen Winkel berechnen Der Sinussatz Das Verhältnis der Längen zweier Seiten ist gleich dem Verhältnis der Sinuswerte ihrer gegenüberliegenden Winkel. Seitenlängen berechnen Mit dem Sinussatz kannst du aus zwei Winkeln und der Länge einer der beiden […]
Vom Einheitskreis zur Winkelfunktion Der Graph der Tangensfunktion Periodizität Symmetrien von Tangens Trigonometrische Gleichungen lösen Vom Einheitskreis zur Winkelfunktion Die Bezeichnung "Tangens" ergibt sich aus dem Begriff Tangente. Der Tangens entspricht der Länge der pinken Strecke, die auf der Tangente des Einheitskreises im Punkt 1 | 0 liegt. Mit Hilfe des zweiten Strahlensatzes kannst du […]
Vom Einheitskreis zur Winkelfunktion Der Graph der Sinusfunktion Der Graph der Kosinusfunktion Periodizität Symmetrien von Sinus und Kosinus Trigonometrische Gleichungen lösen Vom Einheitskreis zur Winkelfunktion Die Bezeichnung „Sinus“ ist lateinisch und bedeutet Bogen. Bewegst du einen Punkt P auf dem Einheitskreis gegen den Uhrzeigersinn und trägst zu jedem Drehwinkel α die y-Koordinate des Punktes P […]
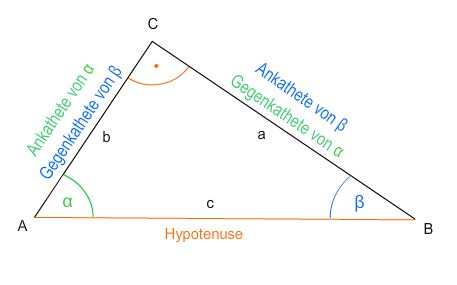
Hier erfährst du, welche Zusammenhänge zwischen den Winkeln in einem rechtwinkligen Dreieck bestehen und wie du diese ausnutzen kannst um andere Größen des Dreiecks zu berechnen. Elementare Beziehungen zwischen Sinus und Kosinus sin²(α) + cos²(α) = 1 Der Tangens als Quotient aus Sinus und Kosinus Der Tangens, Sinus und Kosinus von 45°, 30° und 60° […]
Hier erfährst du, unter welchen Voraussetzungen für die Berechnungen in Dreiecken die Anwendung des Sinussatzes oder die des Kosinussatzes die bessere Strategie ist. Den richtigen Satz benutzen Alle Größen im Dreieck berechnen Den richtigen Satz benutzen Kennst du mindestens drei Größen (Seitenlängen und/oder Winkel) in einem beliebigen Dreieck, dann kannst du mindestens eineweitere Größe berechnen, […]
Die allgemeine Form der Gleichung Verschiebung entlang y-Achse Die Amplitude: Streckung oder Stauchung der Sinuskurve in y-Richtung Die Phase: Verschiebung der Sinuskurve in x-Richtung Die Periode: Streckung oder Stauchung der Sinuskurve in x-Richtung Kombination verschiedener Parameter Die allgemeine Form der Gleichung Du kennst die normale Sinuskurve mit y = sin(x). Durch die Verwendung von Parametern […]

