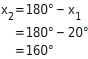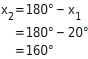Trigonometrie am Einheitskreis
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, wie du Sinus und Kosinus auch für Winkel, die größer sind als
, berechnen kannst.
Sinus und Kosinus am Einheitskreis
Zu jedem Winkel
zwischen
und
gehört ein Punkt P auf dem
mit den
.
Es wird definiert:
Dabei ist
der Winkel zwischen der positiven x-Achse und dem Radius 0P.
Betrachte den Punkt P auf dem Einheitskreis mit den Koordinaten
.
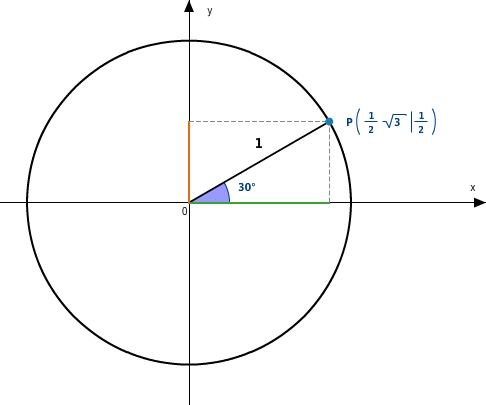 Der zugehörige Winkel
beträgt
.
Der zugehörige Winkel
beträgt
.
 Der zugehörige Winkel
beträgt
.
Der zugehörige Winkel
beträgt
.
Betrachte den Punkt Q auf dem Einheitskreis mit den Koordinaten
.
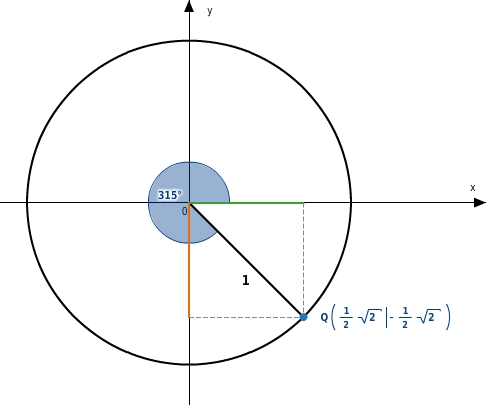 Der zugehörige Winkel
beträgt
.
Der zugehörige Winkel
beträgt
.
 Der zugehörige Winkel
beträgt
.
Der zugehörige Winkel
beträgt
.
Betrachte die Punkte
,
,
und
auf dem Einheitskreis.
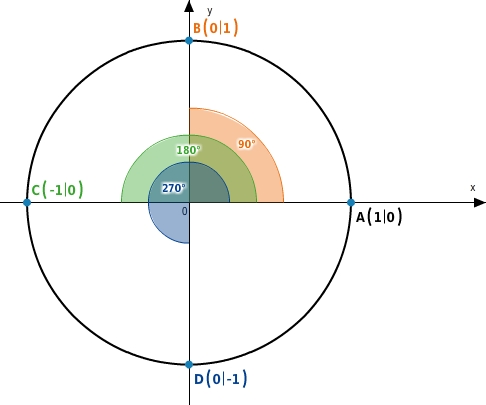 Hier gilt:
Hier gilt:
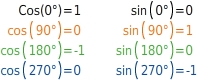
 Hier gilt:
Hier gilt:
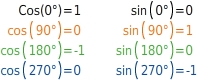
Symmetrien an der x-Achse
Symmetrien an der x-Achse:
Spiegelst du den Punkt
an der x-Achse, dann erhälst du den Punkt P' mit den Koordinaten
.
Liegt der zum Punkt P gehörige Winkel
zwischen
und
, dann ist der zum Punkt P' gehörige Winkel
.
Wegen
und
gilt dann:
und
.
Merksatz 1:
Für jeden Winkel
zwischen
und
gilt:
und
Für einen Winkel
gilt:
.
Also:
und

Für einen Winkel
gilt:
.
Also:
und


Symmetrien an der y-Achse
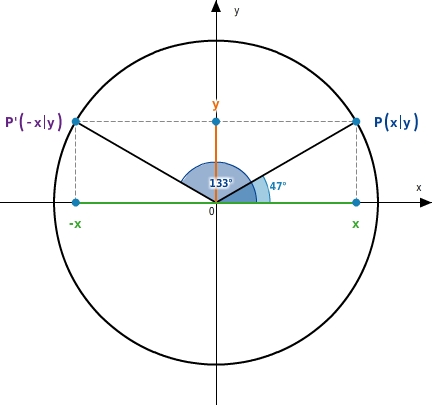
Symmetrien an der y-Achse:
Spiegelst du den Punkt
an der y-Achse, dann erhälst du den Punkt P' mit den Koordinaten
.
Liegt der zum Punkt P gehörige Winkel
zwischen
und
, dann ist der zum Punkt P' gehörige Winkel
.
Wegen
und
gilt dann:
und
.
Merksatz 2:
Für jeden Winkel
zwischen
und
gilt:
und
Für einen Winkel
gilt:
.
Also:
und

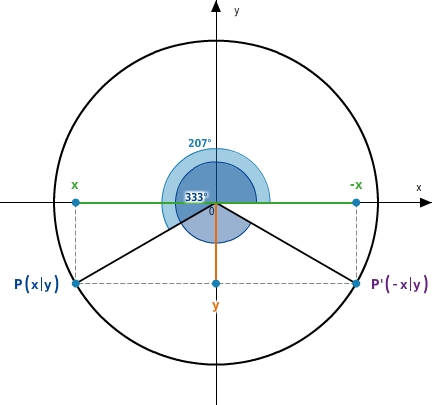
Liegt der zum Punkt P gehörige Winkel
zwischen
und
, dann ist der zum Punkt P' gehörige Winkel
α - 180 ° .
Wegen
und
gilt dann:
und
.
Für einen Winkel
gilt:
.
Also:
und

Symmetrien am Ursprung
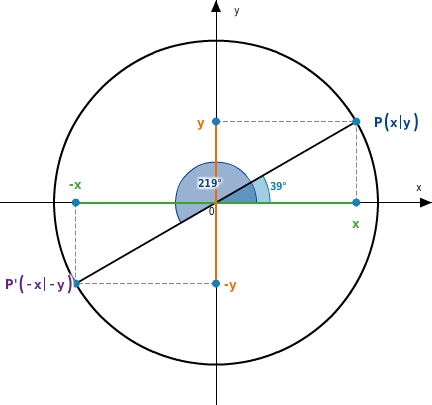
Spiegelst du den Punkt
am Ursprung, dann erhälst du den Punkt P' mit den Koordinaten
. Diese Spiegelung entspricht einer Drehung um
.
Liegt der zum Punkt P gehörige Winkel
zwischen
und
, dann ist der zum Punkt P' gehörige Winkel
.
Wegen
und
gilt dann:
und
.
Merksatz 3:
Für jeden Winkel
zwischen
und
gilt:
und
Für einen Winkel
gilt:
.
Also:
und

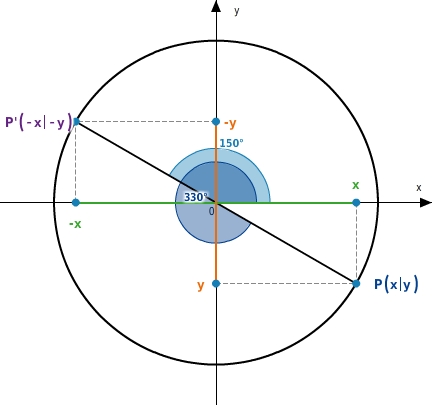
Liegt der zum Punkt P gehörige Winkel
zwischen
und
, dann ist der zum Punkt P' gehörige Winkel
.
Wegen
und
gilt dann:
und
.
Für einen Winkel
gilt:
.
Also:
und

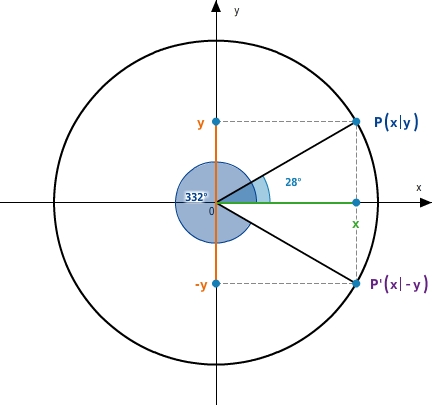
Negative Winkel
Zu jedem Punkt
auf dem Einheitskreis gehört stets ein positiver Winkel
und ein negativer Winkel
, denn du erreichst jeden Punkt durch die Drehung des Punktes
um den Koordinatenursprung sowohl gegen als auch mit dem Uhrzeigersinn.
Bei Drehung gegen den Uhrzeigersinn erhälst du den positiven Winkel
. Bei Drehung im Uhrzeigersinn erhälst du den negativen Winkel
.
Es gilt dann
.
Aus diesem Grund gibt dir dein Taschenrechner einen negativen Winkel
aus, wenn du z.B. die Taste 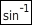 für eine negative Zahl b anwendest.
Den zugehörigen Winkel
erhältst du dann mit
für eine negative Zahl b anwendest.
Den zugehörigen Winkel
erhältst du dann mit

Merksatz 4:
Für jeden Winkel
zwischen
und
gilt:
und
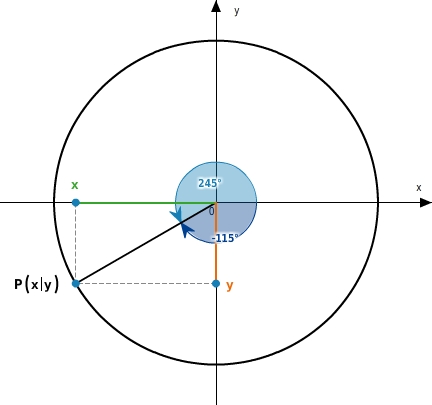
Für einen Winkel
gilt:
.
Also:
und
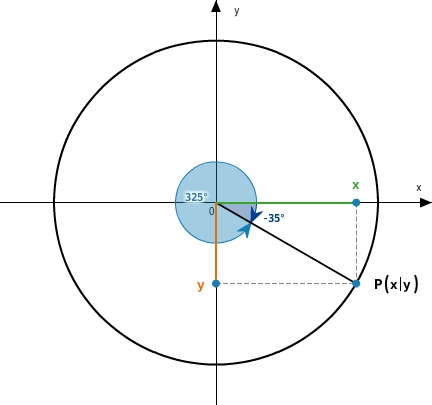

Für einen Winkel
gilt:
.
Also:
und

Lösen trigonometrischer Gleichungen
Da Sinus und Kosinus für verschiedene Winkel die gleichen Werte annehmen können, gibt es für Gleichungen der Form
oder
manchmal mehr als eine Lösung zwischen
und
.
Hast du eine Lösung gefunden, so kannst du die zweite Lösung mit den Symmetrien für Sinus und Kosinus leicht ausrechnen.
Mit der Taste 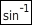 deines Taschenrechners erhältst du
≈
Wegen
ist
deines Taschenrechners erhältst du
≈
Wegen
ist