Berechnungen an Figuren und Körpern
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit den Winkelfunktionen unzugängliche Streckenlängen und Winkel in Figuren und Körpern berechnen kannst.
Winkelfunktionen und Seitenverhältnisse
Je nach Wahl des Winkels bekommen die Seiten im rechtwinkligen Dreieck „neue Namen“.
 Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, Kosinus und Tangens für jeden der beiden spitzen Winkel
und ß.
Der Sinus eines Winkels ist das Längenverhältnis von Gegenkathete zu Hypotenuse:
Der Kosinus eines Winkels ist das Längenverhältnis von Ankathete zu Hypotenuse:
Der Tangens eines Winkels ist das Längenverhältnis von Gegenkathete zu Ankathete:
Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, Kosinus und Tangens für jeden der beiden spitzen Winkel
und ß.
Der Sinus eines Winkels ist das Längenverhältnis von Gegenkathete zu Hypotenuse:
Der Kosinus eines Winkels ist das Längenverhältnis von Ankathete zu Hypotenuse:
Der Tangens eines Winkels ist das Längenverhältnis von Gegenkathete zu Ankathete:
 Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, Kosinus und Tangens für jeden der beiden spitzen Winkel
und ß.
Der Sinus eines Winkels ist das Längenverhältnis von Gegenkathete zu Hypotenuse:
Der Kosinus eines Winkels ist das Längenverhältnis von Ankathete zu Hypotenuse:
Der Tangens eines Winkels ist das Längenverhältnis von Gegenkathete zu Ankathete:
Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, Kosinus und Tangens für jeden der beiden spitzen Winkel
und ß.
Der Sinus eines Winkels ist das Längenverhältnis von Gegenkathete zu Hypotenuse:
Der Kosinus eines Winkels ist das Längenverhältnis von Ankathete zu Hypotenuse:
Der Tangens eines Winkels ist das Längenverhältnis von Gegenkathete zu Ankathete:
 Also:
und
Also:
und
Die Winkelfunktionen werden auch trigonometrische Funktionen genannt (griechisch „Trigonon“ = „ Dreieck“ und „Metron“=“Maß“). Sinus und Kosinus eines Winkels sind immer kleiner als 1, denn die Hypotenuse (im Nenner) ist die längste Seite im Dreieck.Ist der Tangens von α kleiner als 1, dann ist der Tangens von β größer als 1 und umgekehrt.
Lösen von Anwendungsaufgaben Schritt für Schritt
Gegeben ist der Quader mit den Kantenlängen a =
, b =
und c =
.Berechne die Seitenlängen und Winkel des Dreiecks ABH.
 1. Lösungsplan
1. Lösungsplan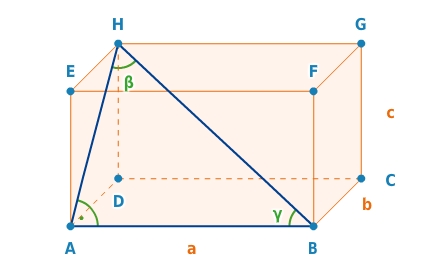 Berechnet werden die Strecken
und
und die Winkel
und
.
Winkel
Nutzen kannst du den Satz des Pythagoras und die Winkelfunktionen.
ist die Diagonale im Rechteck ADHE.
ist die Raumdiagonale des Quaders.
2. Gleichung aufstellen
Berechnet werden die Strecken
und
und die Winkel
und
.
Winkel
Nutzen kannst du den Satz des Pythagoras und die Winkelfunktionen.
ist die Diagonale im Rechteck ADHE.
ist die Raumdiagonale des Quaders.
2. Gleichung aufstellen
 3. Gleichung lösen
3. Gleichung lösen

 1. Lösungsplan
1. Lösungsplan Berechnet werden die Strecken
und
und die Winkel
und
.
Winkel
Nutzen kannst du den Satz des Pythagoras und die Winkelfunktionen.
ist die Diagonale im Rechteck ADHE.
ist die Raumdiagonale des Quaders.
2. Gleichung aufstellen
Berechnet werden die Strecken
und
und die Winkel
und
.
Winkel
Nutzen kannst du den Satz des Pythagoras und die Winkelfunktionen.
ist die Diagonale im Rechteck ADHE.
ist die Raumdiagonale des Quaders.
2. Gleichung aufstellen
 3. Gleichung lösen
3. Gleichung lösen


