Die Winkelfunktion Tangens
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenVom Einheitskreis zur Winkelfunktion
Die Bezeichnung "Tangens" ergibt sich aus dem Begriff Tangente.
 Der Tangens entspricht der Länge der pinken Strecke, die auf der
des Einheitskreises im Punkt
Der Tangens entspricht der Länge der pinken Strecke, die auf der
des Einheitskreises im Punkt 1 | 0 liegt.
Mit Hilfe des
kannst du dir die Definition des Tangens herleiten:
Also:
Beachte aber: Es ist üblich, für das Argument einer Funktion die Variable
zu verwenden.
 Der Tangens entspricht der Länge der pinken Strecke, die auf der
des Einheitskreises im Punkt
Der Tangens entspricht der Länge der pinken Strecke, die auf der
des Einheitskreises im Punkt Der Graph der Tangensfunktion
Die Tangensfunktion ist definiert durch
.
Der Graph lässt sich sowohl für Argumente im Gradmaß als auch im Bogenmaß zeichnen.
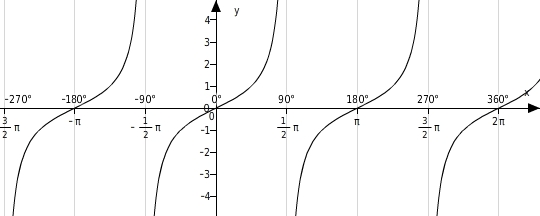 Eigenschaften:
Die Tangensfunktion
Eigenschaften:
Die Tangensfunktion

 Eigenschaften:
Die Tangensfunktion
Eigenschaften:
Die Tangensfunktion

Periodizität
Die Tangensfunktion ist periodisch mit der
. Sie "erbt" diese Eigenschaft von der Sinus- und der Kosinusfunktion.
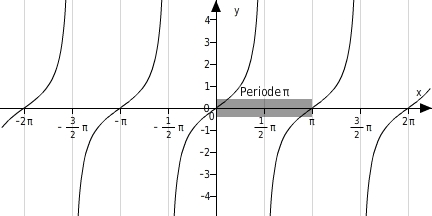 Damit kannst du die gesamte
der Gleichung
angeben, wenn du eine Lösung kennst.
Damit kannst du die gesamte
der Gleichung
angeben, wenn du eine Lösung kennst.
 Damit kannst du die gesamte
der Gleichung
angeben, wenn du eine Lösung kennst.
Damit kannst du die gesamte
der Gleichung
angeben, wenn du eine Lösung kennst.
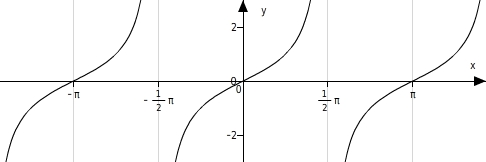
Lösungen im Intervall - π ; π :
Symmetrien von Tangens
Die Tangensfunktion ist
. Das heißt:
und der Graph ist
zum
.


Trigonometrische Gleichungen lösen
Die Periodizität der Tangensfunktion kann dir helfen
der Form
zu lösen.
Da der Wertebereich der Tangensfunktion ℝ ist und die Funktion in jeder Periode alle Werte annimmt, gibt es in jedem Intervall der Länge
eine Lösung dieser Gleichung.
 Mit der Taste
Mit der Taste  des Taschenrechners erhältst du stets Werte im Intervall
des Taschenrechners erhältst du stets Werte im Intervall -90 ° ; 90 ° (
) bzw. im Intervall - 1 2 π ; 1 2 π (
).
Für alle anderen Lösungen addierst du ganzzahlige Vielfache von
zum gefundenen Wert so, dass das Ergebnis im vorgegebenen Intervall liegt.
 Mit der Taste
Mit der Taste
Lösungen im Intervall 5 2 π ; 9 2 π :
Der Taschenrechner zeigt x'≈
Also:
und

