Winkel im Bogenmaß
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenWinkel in Bogenmaß
Zu jedem Mittelpunktswinkel am
gehört ein
auf dem Einheitskreis.
Die Länge des Kreisbogens ist ein Maß für die Größe des Winkels. Dieses wir als Bogenmaß bezeichnet und trägt die Einheit
, abgekürzt
(Modus RAD am Taschenrechner).
 Einem Vollwinkel (
) entspricht das Bogenmaß
.
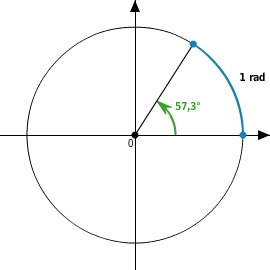
Das Bogenmaß
entspricht einem Winkel von
≈
, also etwa
.
Anders als beim Gradmaß mit der Einheit
(?, Modus DEG am Taschenrechner) wird die Einheit
meist nicht geschrieben.
Einem Vollwinkel (
) entspricht das Bogenmaß
.
Das Bogenmaß
entspricht einem Winkel von
≈
, also etwa
.
Anders als beim Gradmaß mit der Einheit
(?, Modus DEG am Taschenrechner) wird die Einheit
meist nicht geschrieben.
 Einem Vollwinkel (
) entspricht das Bogenmaß
.
Das Bogenmaß
entspricht einem Winkel von
≈
, also etwa
.
Anders als beim Gradmaß mit der Einheit
(?, Modus DEG am Taschenrechner) wird die Einheit
meist nicht geschrieben.
Einem Vollwinkel (
) entspricht das Bogenmaß
.
Das Bogenmaß
entspricht einem Winkel von
≈
, also etwa
.
Anders als beim Gradmaß mit der Einheit
(?, Modus DEG am Taschenrechner) wird die Einheit
meist nicht geschrieben.
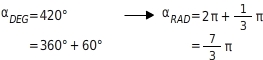
Umrechnen zwischen Grad- und Bogenmaß
Du kannst einen Winkel in Grad (?) oder im Bogenmaß (rad) angeben. Für die Umrechnung gilt:
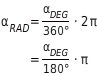
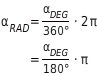
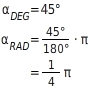
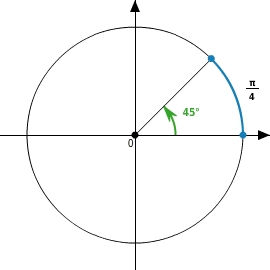 Bei gegebenem Bogenmaß (in
) berechnest du das Gradmaß des Winkels, indem du die Formel nach
umstellst:
Bei gegebenem Bogenmaß (in
) berechnest du das Gradmaß des Winkels, indem du die Formel nach
umstellst:
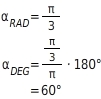
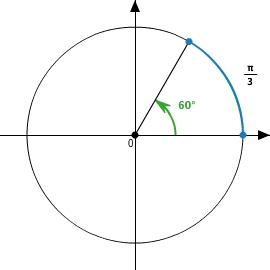
Wichtige Umrechnungen:


Winkel über 2π und negative Winkel
Wird ein Ursprungsstrahl von der x-Achse aus (Winkel
) um den Kreismittelpunkt gegen den Uhrzeigersinn gedreht, entstehen positive Winkel. Je nachdem wie weit gedreht wird, können dabei auch Winkel größer
entstehen.
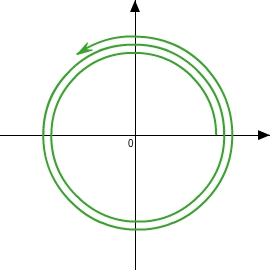

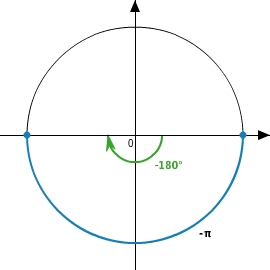
 Bei einer Drehung im Uhrzeigersinn entstehen negative Winkel.
Auch negative Winkel kannst du im Bogenmaß angeben.
Bei einer Drehung im Uhrzeigersinn entstehen negative Winkel.
Auch negative Winkel kannst du im Bogenmaß angeben.