Rechnen mit Bruchtermen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, wie du Bruchterme kürzen, erweitern, addieren, subtrahieren, multiplizieren und dividieren kannst. Mit Bruchtermen rechnest du genauso wie mit Brüchen, nur dass hier auch Variablen vorkommen.
Außerdem wird dir gezeigt, wie du einen Definitionsbereich bestimmen kannst, auf dem die Bruchterme vor und nach der Umformung äquivalent sind, denn beim Umformen eines Bruchterms kann sich der Definitionsbereich ändern.
Kürzen
Einen Bruchterm kannst du kürzen, wenn Zähler und Nenner einen gemeinsamen Faktor haben.
Der Definitionsbereich eines Bruchterms kann sich durch das Kürzen ändern.Der Definitionsbereich, in dem beide Bruchterme äquivalent sind, besteht aus allen Zahlen, für die beide Bruchterme definiert sind.
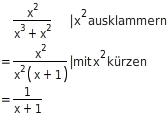 Die Bruchterme
und
sind jeweils für
nicht definiert.
ist aber auch für
nicht definiert,
hingegen schon.
Die beiden Bruchterme sind also für alle
∈ ℚ {-1; 0} definiert und äquivalent.
Die Bruchterme
und
sind jeweils für
nicht definiert.
ist aber auch für
nicht definiert,
hingegen schon.
Die beiden Bruchterme sind also für alle
∈ ℚ {-1; 0} definiert und äquivalent.
 Der Bruchterm
ist für
nicht definiert.Der Term
ist auf ganz ℚ definiert.
Die beiden Bruchterme sind also für alle
∈ ℚ {3} definiert und äquivalent.
Der Bruchterm
ist für
nicht definiert.Der Term
ist auf ganz ℚ definiert.
Die beiden Bruchterme sind also für alle
∈ ℚ {3} definiert und äquivalent.
Kürze den Bruchterm
so weit wie möglich und gib anschließend an, für welchen Definitionsbereich D beide Bruchterme (vor und nach der Umformung) äquivalent sind.
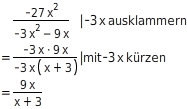
Bruchterm kürzen
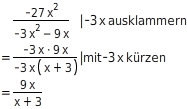
Definitionsbereich bestimmen
Da
für
und
, ist der Bruchterm
für alle
∈ ℚ {-3; 0} definiert.Da
für
, ist der Bruchterm
für alle
∈ ℚ {-3} definiert.Beide Bruchterme sind also für
≠
und
≠ 0 äquivalent.
D = ℚ {-3; 0}
Dividierst du Zähler und Nenner nur durch eine Zahl, ändert sich der Definitionsbereich nicht.
Gegeben ist der Bruchterm
.Kürze so weit wie möglich und bestimme den Definitionsbereich.

Bruchterm kürzen

Definitionsbereich D bestimmen
für
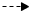 Der Bruchterm
ist nur für
nicht definiert.
für
Der Bruchterm
ist nur für
nicht definiert.
für
 Der Bruchterm
ist nur für
nicht definiert.
Der Definitionsbereich beider Bruchterme ist gleich (ℚ {
}), also sind beide Bruchterme in diesem Definitionsbereich äquivalent.
Der Bruchterm
ist nur für
nicht definiert.
Der Definitionsbereich beider Bruchterme ist gleich (ℚ {
}), also sind beide Bruchterme in diesem Definitionsbereich äquivalent.
D = ℚ {
}
Erweitern
Einen Bruchterm erweiterst du, indem du Zähler und Nenner mit dem gleichen Term multiplizierst.Achte darauf, dass du manchmal Klammern verwenden musst.
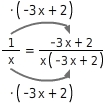
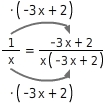
Erweitere den Term
auf den Nenner
x + 2 und gib anschließend den Definitionsbereich an, für den beide Terme (vor und nach der Umformung) äquivalent sind.
Erweitern
Um den Bruchterm auf den Nenner
x + 2 zu erweitern, multiplizierst du Nenner und Zähler mit
.Achte auf die Klammern.
Definitionsbereich D bestimmen
Der Bruchterm
ist für alle
∈ ℚ {0} definiert.
Der Bruchterm
ist für alle
∈ ℚ {
;
} definiert.
Beide Bruchterme sind also für
≠
und
≠
äquivalent.
D = ℚ {
,0}
Erweitere den Term
auf den Nenner
x + 1 und gib anschließend den Definitionsbereich an, für den beide Terme (vor und nach der Umformung) äquivalent sind.
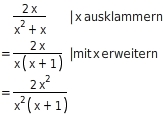 Da
, multiplizierst du Zähler und Nenner nur mit
.
Da
, multiplizierst du Zähler und Nenner nur mit
.
Erweitern
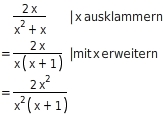 Da
, multiplizierst du Zähler und Nenner nur mit
.
Da
, multiplizierst du Zähler und Nenner nur mit
.
Definitionsbereich D bestimmen
Beide Bruchterme sind für alle
∈ ℚ {
;
} definiert.
D = ℚ {
,
}
Hauptnenner bilden
Der Hauptnenner zweier Bruchterme ist das kleinste gemeinsame Vielfache der vorhandenen Nenner.
Um den Hauptnenner zu bilden, zerlegst du alle Nenner in Faktoren und multiplizierst die höchsten vorkommenden Potenzen jedes Faktors miteinander.
Bestimme den Hauptnenner der Bruchterme
und
.
x + 1 enthält die Faktoren
und
, der Nenner des zweiten Bruchterms ist also im Nenner des ersten Bruchterms als Faktor enthalten.Also ist
x + 1 kleinstes gemeinsames Vielfaches beider Nenner und damit Hauptnenner.
Hauptnenner bestimmen
Der Hauptnenner ist
x + 1 .
Bestimme den Hauptnenner der Bruchterme
und
.
Hauptnenner bestimmen
Du zerlegst die Nenner in Faktoren.
und
Du bildest das Produkt der Faktoren mit den jeweils höchsten Exponenten.
x + 1
Der Hauptnenner ist
x + 1 .
Bestimme den Hauptnenner der Bruchterme
und
.
Hauptnenner bestimmen
Beide Nenner sind nicht weiter zerlegbar: Sie entsprechen selbst jeweils einem Faktor.
Du bildest daher das Produkt beider Nenner.
x 2 + 1
x + 3
Der Hauptnenner ist x 2 + 1 x + 3 .
Addieren und subtrahieren
Du addierst bzw. subtrahierst zwei oder mehrere Bruchterme, indem du:
 Achte darauf, dass du in manchen Fällen Klammern verwenden musst.
Der Definitionsbereich, in dem die Bruchterme äquivalent sind, kann durch die Umformung verändert werden.
Achte darauf, dass du in manchen Fällen Klammern verwenden musst.
Der Definitionsbereich, in dem die Bruchterme äquivalent sind, kann durch die Umformung verändert werden.
 Achte darauf, dass du in manchen Fällen Klammern verwenden musst.
Der Definitionsbereich, in dem die Bruchterme äquivalent sind, kann durch die Umformung verändert werden.
Achte darauf, dass du in manchen Fällen Klammern verwenden musst.
Der Definitionsbereich, in dem die Bruchterme äquivalent sind, kann durch die Umformung verändert werden.
Addiere die Bruchterme
und
.
Addieren
Beide Bruchterme sind gleichnamig, sie haben denselben Nenner. Also addierst du die Zähler und lässt den Nenner unverändert.
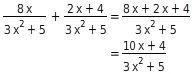
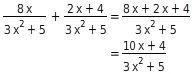
Addiere die Bruchterme
und
.
Addieren
Die Bruchterme sind nicht gleichnamig, du erweiterst sie auf den Hauptnenner x + 2 x + 1 .
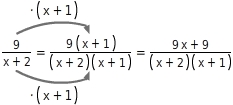
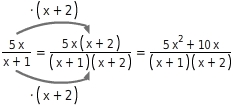 Jetzt addierst du die Zähler.
Jetzt addierst du die Zähler.
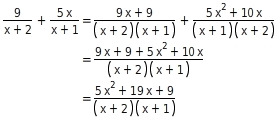
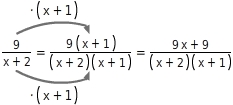
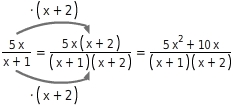 Jetzt addierst du die Zähler.
Jetzt addierst du die Zähler.
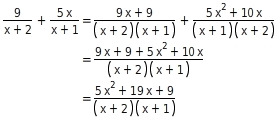
Subtrahiere
von
.
Subtrahieren
Die Bruchterme sind nicht gleichnamig, du erweiterst sie auf den Hauptnenner
.
 bleibt unverändert.
Jetzt subtrahierst du die Zähler.
bleibt unverändert.
Jetzt subtrahierst du die Zähler.

 bleibt unverändert.
Jetzt subtrahierst du die Zähler.
bleibt unverändert.
Jetzt subtrahierst du die Zähler.

Vereinfache
.
Zusammenfassen
Du erweiterst 3 mit
.
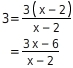 Die Bruchterme sind jetzt gleichnamig.
Die Bruchterme sind jetzt gleichnamig.
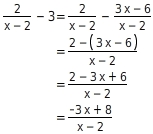
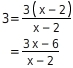 Die Bruchterme sind jetzt gleichnamig.
Die Bruchterme sind jetzt gleichnamig.
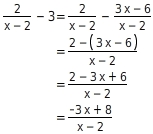
Multiplizieren und dividieren
Du multiplizierst Bruchterme, indem du jeweils die Zähler und die Nenner multiplizierst.
Du dividierst Bruchterme, indem du den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms multiplizierst.
Achte darauf, dass in manchen Fällen Klammern gesetzt werden müssen.
Der Definitionsbereich kann durch die Umformung verändert werden.
Fasse
zusammen und gib anschließend an, für welche Zahlen die Terme äquivalent sind.
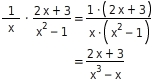
Multiplizieren
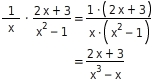
äquivalenz bestimmen
ist für alle x ∈ ℚ bis auf
definiert.
ist für alle x ∈ ℚ bis auf
und
definiert.
Der Definitionsbereich D des Terms
ist also D = ℚ {-1; 0; 1}.
Beide Terme sind also für alle x ∈ ℚ {-1; 0; 1} definiert und äquivalent.
Die Terme sind für alle x ∈ ℚ {-1; 0; 1} definiert und äquivalent.
Berechne
. Gib dafür zunächst den Definitionsbereich D des Terms an.
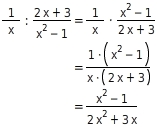
Definitionsbereich angeben
Der Term
besteht aus zwei Termen, dem Term
und dem Term
.
ist für alle x ∈ ℚ bis auf
definiert.
ist für alle x ∈ ℚ bis auf
und
definiert.
Da durch
dividiert wird, darf
nicht null sein.
für
.
Also ist der Term
für alle x ∈ ℚ {-1,
, 0, 1} definiert.
D = ℚ {-1,
, 0, 1}
Kehrwert bilden
Der Kehrwert von
ist
.
Multiplizieren
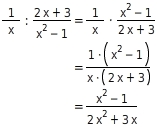
Multipliziere
.
Multiplizieren
Hier kannst du vor dem Multiplizieren kürzen.
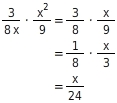
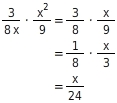
Potenzrechnung
Eine Potenz mit negativem Exponenten ist der Kehrwert der Potenz mit betragsgleichem positiven Exponenten und gleicher Basis, d.h. man schreibt
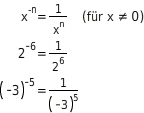 Die Regeln zum Multiplizieren und Dividieren von Potenzen mit positiven Exponenten gelten auch für Potenzen mit negativen Exponenten:
Die Regeln zum Multiplizieren und Dividieren von Potenzen mit positiven Exponenten gelten auch für Potenzen mit negativen Exponenten:

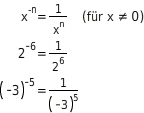 Die Regeln zum Multiplizieren und Dividieren von Potenzen mit positiven Exponenten gelten auch für Potenzen mit negativen Exponenten:
Die Regeln zum Multiplizieren und Dividieren von Potenzen mit positiven Exponenten gelten auch für Potenzen mit negativen Exponenten:

Vereinfache
.
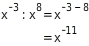
Dividieren
Vereinfache
.
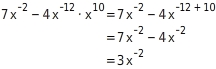
Zusammenfassen
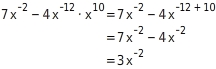
Vereinfache
.
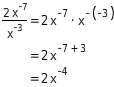
Dividieren