Zufallsexperimente und Baumdiagramme
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie man mit Hilfe von Baumdiagrammen die Wahrscheinlichkeiten von Ereignissen mehrstufiger Zufallsexperimente berechnen kann.
Erweiterung von Baumdiagrammen zu Wahrscheinlichkeitsbäumen
Baumdiagramme können durch eine kleine Erweiterung sehr geschickt zur Berechnung von Wahrscheinlichkeiten von Ereignissen mehrstufiger Zufallsexperimente benutzt werden.
Dazu trägst du an den Zweigen die jeweiligen Wahrscheinlichkeiten ein, mit denen das zum Zweig gehörige Ergebnis des Teilexperimentes eintritt. Diese Wahrscheinlichkeiten nennt man kurz Zweigwahrscheinlichkeiten.
Ein Baumdiagramm, das Zweigwahrscheinlichkeiten enthält, nennt man auch kurz Wahrscheinlichkeitsbaum. üblicherweise gibt man alle Zweigwahrscheinlichkeiten entweder komplett als Brüche oder Dezimalzahlen an.
Zweimaliges Ziehen aus einer Urne ohne Zurücklegen
Du kannst den Wahrscheinlichkeitsbaum zu folgendem Zufallsexperiment konstruieren:Aus der abgebildeten Urne werden nacheinander 2 Kugeln gezogen, ohne sie zurückzulegen.Ein passendes Baumdiagramm ist zum Beispiel:




Beachte hierbei, dass die Farbe Blau nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden. Daher gibt es keinen Zweig zu Blau, nachdem Blau gezogen wurde.
Jeder Zweig im Baumdiagramm entspricht einem Ergebnis eines der beiden Teilexperimente „Ziehen der ersten Kugel aus der Urne“ bzw. „Ziehen der zweiten Kugel aus der Urne „.
Eine Zweigwahrscheinlichkeit ist die Wahrscheinlichkeit dafür, dass das zum jeweiligen Zweig gehörige Ergebnis eintritt.
Beim Ziehen der ersten Kugel sind die möglichen Ergebnisse  ,
,  und
und  .
Beim ersten Ziehen kann jede Kugel mit derselben Wahrscheinlichkeit (
) gezogen werden.
Daher kannst du die Wahrscheinlichkeiten der Ergebnisse
.
Beim ersten Ziehen kann jede Kugel mit derselben Wahrscheinlichkeit (
) gezogen werden.
Daher kannst du die Wahrscheinlichkeiten der Ergebnisse  ,
,  und
und  mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten berechnen:
Erste Ziehung
Wahrscheinlichkeit von Teilergebnis
mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten berechnen:
Erste Ziehung
Wahrscheinlichkeit von Teilergebnis  :
Wahrscheinlichkeit von Teilergebnis
:
Wahrscheinlichkeit von Teilergebnis  :
=
Wahrscheinlichkeit von Teilergebnis
:
=
Wahrscheinlichkeit von Teilergebnis  :
:
 Die Wahrscheinlichkeiten der Teilergebnisse
Die Wahrscheinlichkeiten der Teilergebnisse  ,
,  und
und  für die zweite Ziehung sind nun abhängig vom Ausgang der ersten Ziehung. Je nachdem fehlt nun eine der Kugeln der Farbe
für die zweite Ziehung sind nun abhängig vom Ausgang der ersten Ziehung. Je nachdem fehlt nun eine der Kugeln der Farbe  ,
,  bzw.
bzw.  .
Zweite Ziehung
Falls die erste Ziehung
.
Zweite Ziehung
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
Wahrscheinlichkeit von Teilergebnis
:
Wahrscheinlichkeit von Teilergebnis  :
=
Wahrscheinlichkeit von Teilergebnis
:
=
Wahrscheinlichkeit von Teilergebnis  :
Falls die erste Ziehung
:
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
=
Wahrscheinlichkeit von Teilergebnis
:
=
Wahrscheinlichkeit von Teilergebnis  :
Wahrscheinlichkeit von Teilergebnis
:
Wahrscheinlichkeit von Teilergebnis  :
Falls die erste Ziehung
:
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
=
Wahrscheinlichkeit von Teilergebnis
:
=
Wahrscheinlichkeit von Teilergebnis  :
=
Nach dem Eintragen aller Zweigwahrscheinlichkeiten sieht der Wahrscheinlichkeitsbaum wie folgt aus:
:
=
Nach dem Eintragen aller Zweigwahrscheinlichkeiten sieht der Wahrscheinlichkeitsbaum wie folgt aus:

 Die Wahrscheinlichkeiten der Teilergebnisse
Die Wahrscheinlichkeiten der Teilergebnisse 
Die Summenregel für Zweige
Die von einem Knoten ausgehenden Zweige führen zu den Ergebnissen des zugehörigen Teilexperimentes. Die Zusammenfassung aller möglichen Ergebnisse eines Teilexperimentes stellt das sichere Ereignis dar, denn für jeden möglichen Ausgang des Teilexperimentes ist ein Knoten und somit auch ein Zweig vorhanden.
Somit ergibt sich:
Summenregel für Zweige: Die Summe der Zweigwahrscheinlichkeiten der von einem Knoten abgehenden Zweige ist 1.
Betrachte zum Beispiel den Wahrscheinlichkeitsbaum zum Experiment „Zweimaliges Ziehen einer Kugel aus der abgebildeten Urne ohne Zurücklegen“.




Die vom Wurzelknoten ausgehenden Zweige führen zu den Knoten, die die Ergebnisse des ersten Teilexperiments - das Ziehen der ersten Kugel - darstellen. Die Summe der Zweigwahrscheinlichkeiten ist hierbei
.
Betrachte nun die Zweige, die das zweite Teilexperiment beschreiben:
Je nach Ausgang des ersten Teilexperimentes gibt es verschiedene Wahrscheinlichkeiten für die Farben  ,
,  und
und  , dennoch ergeben die Summen der Zweigwahrscheinlichkeiten immer 1:
Falls die erste Ziehung
, dennoch ergeben die Summen der Zweigwahrscheinlichkeiten immer 1:
Falls die erste Ziehung  lieferte:
= 1
Falls die erste Ziehung
lieferte:
= 1
Falls die erste Ziehung  lieferte:
= 1
Falls die erste Ziehung
lieferte:
= 1
Falls die erste Ziehung  lieferte:
= 1
lieferte:
= 1
Ergänze am Baumdiagramm die fehlenden Zweigwahrscheinlichkeiten. Gib die Wahrscheinlichkeiten als gekürzte Brüche ein.

Wahrscheinlichkeiten ergänzen
Gemäß der Summenregel muss die Summe der Zweigwahrscheinlichkeiten aller von einem Knoten ausgehenden Zweige 1 sein.
So ermittelst du:

Die Produktregel für Pfade
Zu jedem Endknoten eines Baumdiagramms führt von der Wurzel ausgehend eine Kette von Zweigen: ein sogenannter Pfad.
Ein Pfad beschreibt ein mögliches Ergebnis des mehrstufigen Zufallsexperimentes.
Die Pfadwahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein solches Ergebnis eintritt. Sie ist das Produkt aus den Zweigwahrscheinlichkeiten der zum Pfad gehörigen Zweige.
Produktregel für PfadePfadwahrscheinlichkeiten sind die Produkte der Zweigwahrscheinlichkeiten der zu einem Pfad gehörigen Zweige.
Pfade in einem Baumdiagramm und die zugehörigen Ergebnisse
Aus der abgebildeten Urne werden nacheinander 2 Kugeln gezogen, ohne sie zurückzulegen. Im Baumdiagramm sind die Ergebnisse und zugehörigen Pfade zum Ereignis „Genau eine Kugel hat die Farbe Gelb“ hervorgehoben.
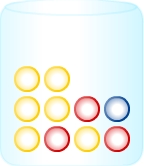



Beachte, dass zum Beispiel 
 und
und 
 verschiedene Ergebnisse sind.
verschiedene Ergebnisse sind.
Um die Wahrscheinlichkeiten einzelner Ergebnisse eines mehrstufigen Zufallsexperimentes zu berechnen, ermittelst du die zugehörigen Pfadwahrscheinlichkeiten mit Hilfe der Produktregel.
Ergänze am Baumdiagramm die fehlenden Pfadwahrscheinlichkeiten. Gib die Wahrscheinlichkeiten als gekürzte Brüche ein.

Pfadwahrscheinlichkeiten ergänzen
Die Pfadwahrscheinlichkeiten sind die Wahrscheinlichkeiten der einzelnen möglichen Ergebnisse des mehrstufigen Zufallsexperimentes.
Die Produktregel besagt: Du berechnest die Pfadwahrscheinlichkeit für ein Ergebnis des mehrstufigen Zufallsexperimentes, indem du die Wahrscheinlichkeiten der Zweige multiplizierst, die den Pfad zu diesem Ergebnis bilden.
Auf diese Weise ermittelst du:
P(
 ) =
P(
) =
P(
 ) =
P(
) =
P(
 ) =
P(
) =
P(
 ) =
) =

Ereigniswahrscheinlichkeiten mit Wahrscheinlichkeitsbäumen berechnen
Wenn du ein Baumdiagramm zu einem Wahrscheinlichkeitsbaum erweitert hast, kannst du diesen Baum nutzen, um Wahrscheinlichkeiten von Ereignissen des zugehörigen Zufallsexperimentes zu berechnen.
Dazu markierst du alle Ergebnisse des mehrstufigen Zufallsexperimentes, die zu einem interessierenden Ereignis gehören und ermittelst für diese die zugehörigen Pfadwahrscheinlichkeiten.
Zum Schluss addierst du diese Pfadwahrscheinlichkeiten.
Aus der abgebildeten Urne werden nacheinander 2 Kugeln gezogen, ohne sie zurückzulegen. Ein zugehöriger Wahrscheinlichkeitsbaum ist angegeben:

 Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
 ;
; 
 ;
; 
 ;
; 

 Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
 ) =
P(
) =
P(
 ) =
P(
) =
P(
 ) =
P(
) =
P(
 ) =
Diese Pfadwahrscheinlichkeiten schreibst du neben die zugehörigen Ergebnisse.
) =
Diese Pfadwahrscheinlichkeiten schreibst du neben die zugehörigen Ergebnisse.
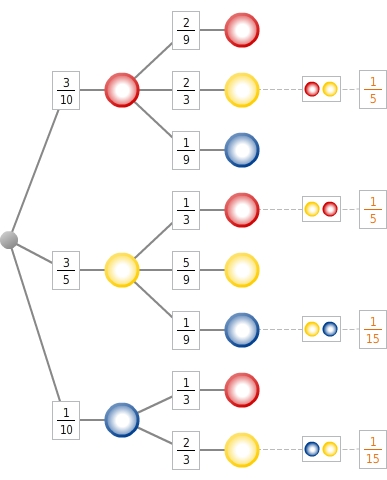 Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:
Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:


 Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest: Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P( Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:
Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:

Die beiden abgebildeten Glücksräder werden jeweils einmal gedreht. Zuerst wird das linke, dann das rechte Glücksrad gedreht.

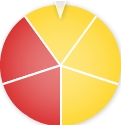 Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.

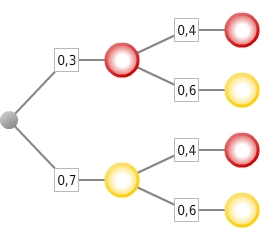
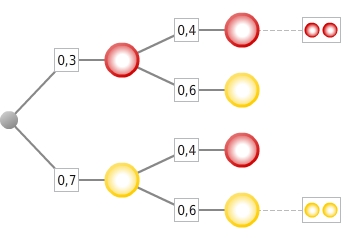

 Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Baumdiagramm konstruieren
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad“ entsprechen:
 und
und  .
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle.
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad“ führen:
.
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle.
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad“ führen:
 und
und  .
Wiederum spielt dabei die Reihenfolge der Zweige bzw. Knoten keine Rolle.
.
Wiederum spielt dabei die Reihenfolge der Zweige bzw. Knoten keine Rolle.

Zweigwahrscheinlichkeiten ergänzen
Eine Zweigwahrscheinlichkeit ist die Wahrscheinlichkeit dafür, dass das zum jeweiligen Zweig gehörige Ergebnis eintritt.
Beim Drehen sowohl des linken Glücksrades als auch des rechten Glücksrades sind die möglichen Ergebnisse  und
und  .
Da für die beiden Glücksräder jeder Sektor mit gleicher Wahrscheinlichkeit (
bzw.
) gedreht werden kann, berechnest du die Wahrscheinlichkeiten der Teilergebnisse
.
Da für die beiden Glücksräder jeder Sektor mit gleicher Wahrscheinlichkeit (
bzw.
) gedreht werden kann, berechnest du die Wahrscheinlichkeiten der Teilergebnisse  und
und  für die beiden Glücksräder mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten:
Drehen des linken Glücksrades:Wahrscheinlichkeit von Teilergebnis
für die beiden Glücksräder mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten:
Drehen des linken Glücksrades:Wahrscheinlichkeit von Teilergebnis  :
= 0,3Wahrscheinlichkeit von Teilergebnis
:
= 0,3Wahrscheinlichkeit von Teilergebnis  :
= 0,7
Drehen des rechten Glücksrades:Wahrscheinlichkeit von Teilergebnis
:
= 0,7
Drehen des rechten Glücksrades:Wahrscheinlichkeit von Teilergebnis  :
= 0,4Wahrscheinlichkeit von Teilergebnis
:
= 0,4Wahrscheinlichkeit von Teilergebnis  :
= 0,6
:
= 0,6

Ergebnisse auswählen
Du ziehst alle diejenigen Ergebnisse an die entsprechenden Positionen im Baum, die zu dem Ereignis E „Die Räder bleiben auf derselben Farbe stehen“ gehören:

 und
und 
 .
.

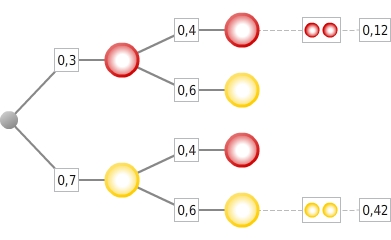
Pfadwahrscheinlichkeiten ermitteln
Du berechnest die Pfadwahrscheinlichkeiten mit Hilfe der Produktregel. Du multiplizierst also die Zweigwahrscheinlichkeiten der Pfade, die zu den zum Ereignis E gehörenden Ergebnissen führen.
P(
 ) = 0,3
0,4 = 0,12P(
) = 0,3
0,4 = 0,12P(
 ) = 0,7
0,6 = 0,42
) = 0,7
0,6 = 0,42

Wahrscheinlichkeit berechnen
Du ermittelst die Wahrscheinlichkeit eines Ereignisses mit Hilfe eines Wahrscheinlichkeitsbaumes, indem du die Pfadwahrscheinlichkeiten der zum Ereignis gehörigen Ergebnisse addierst.
P(E) = P(
 ) + P(
) + P(
 ) = 0,12 + 0,42 = 0,54
) = 0,12 + 0,42 = 0,54
P(E) = 0,54

