Größenvergleich von Brüchen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du Brüche miteinander vergleichen kannst.
Vergleich von gleichnamigen Brüchen
Am einfachsten lassen sich Brüche vergleichen, wenn sie gleichnamig sind. Der größere Zähler gibt dann den größeren Bruch an.
Vergleiche
und
( <, > oder = )
Vergleiche
2 > 1 also
>
und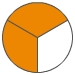 >
> 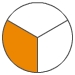
 >
> 
Sortiere die Brüche. Beginne mit dem kleinsten.

Sortieren
Alle Brüche haben den Nenner 9.
<
<
<
<
<
, weil 1 < 2 < 4 < 5 < 7 < 8.

Vergleich von zählergleichen Brüchen
Um zählergleiche Brüche zu vergleichen, betrachtest du deren Nenner. Ein größerer Nenner bedeutet,dass der Zähler in kleinere Teile eingeteilt ist. Somit ist der Bruch insgesamt auch kleiner. Der größere Nenner gibt den kleineren Bruch an.
Vergleiche
und
(<, > oder = )
Vergleiche
8 > 4 also
<
und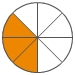 <
< 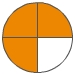
 <
< 
Sortiere die Brüche. Beginne mit dem kleinsten.
Sortieren
Alle Brüche haben den Zähler 5.
, weil 12 > 11 > 9 > 8 > 6.
Der größere Nenner gibt den kleineren Bruch an.
Vergleich von ungleichnamigen Brüchen
Zum Vergleichen kannst du ungleichnamige Brüche gleichnamig machen, indem du sie erweiterst oder kürzt.
Vergleiche
und
(<, > oder = )
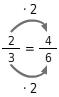
Hauptnenner
Du erweiterst
auf den Hauptnenner 6, indem du Zähler und Nenner mit 2 multiplizierst.

Vergleiche
4 < 5 also
<
und
<
.
Vergleiche
und
(<, > oder = )
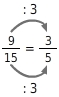
Hauptnenner
Du kürzt
auf den Hauptnenner 5, indem du Zähler und Nenner durch 3 dividierst.

Vergleiche
2 < 3 also
<
und
<
.
Vergleich von gemischten Zahlen
Gemischte Zahlen kannst du miteinander vergleichen, indem du als erstes die ganzen Zahlen miteinander vergleichst. Ist bereits eine der Zahlen größer als die andere, brauchst du die Bruchteile nicht mehr miteinander zu vergleichen.
Sind die ganzen Zahlen gleich groß, so müssen die Bruchteile miteinander verglichen werden.Das kannst du in den drei vorherigen Erklärungen noch mal nachlesen.
Vergleiche
und
(<, > oder = )
Vergleiche
2 < 3, also
<
und

 <
< 




 <
< 




