Periodische Dezimalzahlen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, welche Eigenschaften periodische Dezimalzahlen haben und wie du diese in Brüche umrechnen kannst.
- Was ist eine periodische Dezimalzahl?
- Wie entsteht eine periodische Dezimalzahl?
- Runden einer periodischen Dezimalzahl
- Vergleichen von periodischen Dezimalzahlen
- Reinperiodische und gemischtperiodische Dezimalzahlen
- Reinperiodische Dezimalzahlen in Brüche umwandeln
- Gemischtperiodische Dezimalzahlen in Brüche umwandeln
- Wichtige periodische Dezimalzahlen als Bruch
Was ist eine periodische Dezimalzahl?
Eine periodische Dezimalzahl erkennst du daran, dass sich eine Ziffer oder eine Folge von Ziffern nach dem Komma immer wiederholt. Die Wiederholungen können bei der ersten Nachkommastelle beginnen, sie können aber auch erst später beginnen.
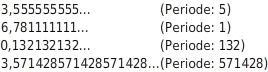
Die Pünktchen zeigen an, dass sich diese Wiederholung endlos fortsetzt.Die sich wiederholenden Ziffern einer periodischen Dezimalzahl nennt man ihre „Periode“.

Um die periodischen Dezimalzahlen leichter aufschreiben zu können, hat man noch eine andere Darstellung eingeführt. Die Periode wird nur einmal aufgeschrieben und darüber wird ein Periodenstrich gesetzt.

Die Anzahl der Ziffern unter dem Periodenstrich wird auch Periodenlänge genannt.
Wie entsteht eine periodische Dezimalzahl?
Periodische Dezimalzahlen entstehen bei der Division mit Rest, wenn du den Rest weiter dividierst. Hat der Divisor nur die Primfaktoren 2 oder 5, so erhältst du eine Dezimalzahl mit endlich vielen Nachkommastellen. Hat der Divisior als Teiler 3 oder 7, 11, …, so erhältst du eine periodische Dezimalzahl.



Runden einer periodischen Dezimalzahl
Um mit periodischen Dezimalzahlen rechnen zu können, ist es hilfreich, sie auf eine geeignete Nachkommastelle zu runden.
Damit du weißt, ob du auf- oder abrunden musst, musst du feststellen, welche Ziffer rechts neben der Rundungsstelle steht.
Runde
auf Zehntel.
Zahlen runden
= 4,88888... Rechts neben der Zehntelstelle steht eine 8, also musst du aufrunden.
... ≈ 4,9
≈ 4,9
Runde
auf Hundertstel.
Zahlen runden
= 6,78111... Rechts neben der Hundertstelstelle steht eine 1, also musst du abrunden.
... ≈ 6,78
≈ 6,78
Runde
auf Tausendstel.
Zahlen runden
= 0,132132132... Rechts neben der Tausendstelstelle steht eine 1, also musst du abrunden.
... ≈ 0,132
≈ 0,132
Runde
auf Hundertstel.
Zahlen runden
= 3,571428571428... Rechts neben der Hundertstelstelle steht eine 1, also musst du abrunden.
... ≈ 3,57
≈ 3,57
Vergleichen von periodischen Dezimalzahlen
Wenn du periodische Dezimalzahlen miteinander oder mit anderen Dezimalzahlen vergleichen möchtest, vergleichst du ihre Stellenwerte miteinander. Du beginnst von links. Der erste unterschiedliche Stellenwert muss verglichen werden.
Liegt dieser erste Stellenwert nicht in der Periode, dann gehst du genauso vor, wie beim Vergleichen von nichtperiodischen Dezimalzahlen.
Vergleiche
und 0,25.
Zahlen vergleichen
und
Die Zehntelwerte sind die ersten unterschiedlichen Stellenwerte. Da
, ist
.
Vergleiche
und 7,51.
Zahlen vergleichen
und
Die Einerstellenwerte sind die ersten unterschiedlichen Stellenwerte.Da
<
, ist
<
.
<
Liegt dieser erste Stellenwert in der Periode, dann löst du die Periode auf, das heißt, du schreibst die periodische Dezimalzahl ohne Periodenstrich.
Vergleiche
und
.
Zahlen vergleichen
Die periodische Dezimalzahl
kann man auch so schreiben: 0,6666666...
und
ist das Gleiche wie:
und
...Die Hundertstelstelle ist die erste Stelle von links, die sich unterscheidet.
Da
, ist
.
Vergleiche
und
.
Zahlen vergleichen
und
ist das Gleiche wie:
... und
...
Die Tausendstelstelle ist die erste Stelle von links, die sich unterscheidet.Da
, ist
.
Reinperiodische und gemischtperiodische Dezimalzahlen
Reinperiodische Dezimalzahlen sind Dezimalzahlen, bei denen die Periode direkt nach dem Komma beginnt.
14,1111... =
0,294294294... =
Gemischtperiodische Dezimalzahlen sind Dezimalzahlen, bei denen zwischen der Periode und dem Komma noch mindestens eine Ziffer steht.
0,16666... =
... =
Reinperiodische Dezimalzahlen in Brüche umwandeln
Reinperiodische und gemischtperiodische Dezimalzahlen werden bei der Umwandlung in Brüche unterschiedlich behandelt.
Bei der Umwandlung reinperiodischer Dezimalzahlen steht im Nenner des gesuchten Bruchs immer 9, 99, 999, … Die Länge der Periode zeigt dir die Anzahl der Neunen im Nenner. In den Zähler des gesuchten Bruchs wird die Zahl unter dem Periodenstrich geschrieben. Steht vor dem Komma eine natürliche Zahl, so erhältst du eine gemischte Zahl mit dieser natürlichen Zahl als Ganze.
Wandle
in einen Bruch um.
Umwandeln
Die Periodenlänge beträgt
also steht eine Neun (9) im Nenner.Die einzige Ziffer in der Periode ist die 4. Die 4 kommt in den Zähler.
Wandle
in einen Bruch um.
Umwandeln
Die Periodenlänge beträgt
also stehen zwei Neunen (99) im Nenner.Die Ziffern der Periode sind 4 und 3. Die 43 kommt in den Zähler.Die 2 Einer vor dem Komma schreibst du als Ganze vor den Bruch.
Gemischtperiodische Dezimalzahlen in Brüche umwandeln
Reinperiodische und gemischtperiodische Dezimalzahlen werden bei der Umwandlung in Brüche unterschiedlich behandelt.
Bei der Umwandlung gemischtperiodischer Dezimalzahlen musst du zunächst aus der gemischtperiodischen Dezimalzahl durch Kommaverschiebung eine reinperiodische Dezimalzahl machen. Dazu multiplizierst du die Zahl mit einer geeigneten Zehnerpotenz.
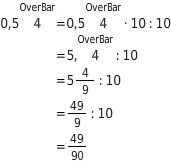
Um aus der gemischtperiodischen Dezimalzahl
, eine reinperiodische zu machen, verschiebst du das Komma um eine Stelle nach rechts, indem du die Zahl mit 10 multiplizierst. Nach dem Umwandeln musst du die Multiplikation wieder rückgängig machen (sonst würde sich der Wert der Zahl ändern). Du musst dazu den Bruch durch 10 dividieren.
Wichtige periodische Dezimalzahlen als Bruch
Periodische Dezimalzahlen, für die du die Darstellung als Bruch auswendig kennen solltest:



