Zylinder
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenEigenschaften von Zylindern
Ein Kreiszylinder (kurz: Zylinder) ist ein geometrischer Körper mit
und parallelen Kreisen als Grund- und Deckfläche.
Beim geraden Zylinder ist die Mantelfläche ein Rechteck.
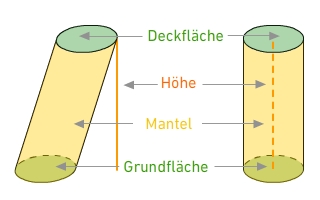 schiefer Zylindergerader Zylinder
schiefer Zylindergerader Zylinder
 schiefer Zylindergerader Zylinder
schiefer Zylindergerader Zylinder
Im Weiteren wird der gerade Kreiszylinder kurz als Zylinder bezeichnet. Ist von einem schiefen Zylinder die Rede, so wird das ausdrücklich erwähnt.
Volumenberechnung
kurz:
Die Grundfläche des Zylinders ist ein Kreis mit
r, daher ergibt sich die spezielle Formel
.
Zylinder mit einer Höhe h von
und einem Radius r von

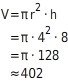

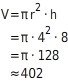
Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Zylinders berechnen.
Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
 und
und
Oberflächenberechnung
kurz:
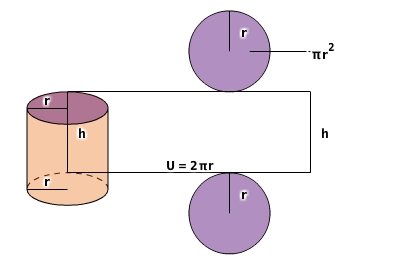
Die Oberfläche eines Zylinders setzt sich zusammen aus Grundfläche G, Deckfläche D und Mantelfläche M.
Grund- und Deckfläche sind gleich groß, also gilt:
Die Grundfläche ist ein
:
Der Mantel eines geraden Zylinders ist ein
mit der Seitenlänge U (Umfang des Kreises) und h (Höhe des Zylinders):
Für den Oberflächeninhalt des Zylinders gilt damit die spezifische Formel:

Zylinder mit einer Höhe h von
und einem Radius r von
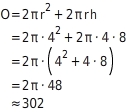

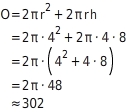
Hohlzylinder
Ein Hohlzylinder entsteht, wenn aus einem Zylinder ein kleinerer Zylinder herausgeschnitten wird.
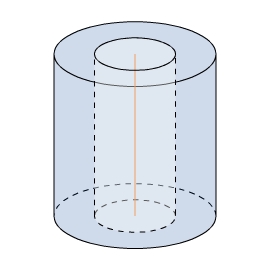

Im Weiteren werden Hohlzylinder betrachtet, bei denen beide Zylinder die gleiche Symmetrieachse haben.
Volumen des Hohlzylinders:
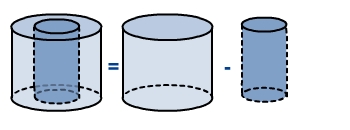 Oberfläche des Hohlzylinders:
• der Mantelfläche
des äußeren Zylinders, • der Mantelfläche
des inneren Zylinders, • der Fläche
des
.
Oberfläche des Hohlzylinders:
• der Mantelfläche
des äußeren Zylinders, • der Mantelfläche
des inneren Zylinders, • der Fläche
des
.
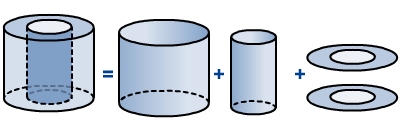
 Oberfläche des Hohlzylinders:
• der Mantelfläche
des äußeren Zylinders, • der Mantelfläche
des inneren Zylinders, • der Fläche
des
.
Oberfläche des Hohlzylinders:
• der Mantelfläche
des äußeren Zylinders, • der Mantelfläche
des inneren Zylinders, • der Fläche
des
.

Funktionale Abhängigkeiten
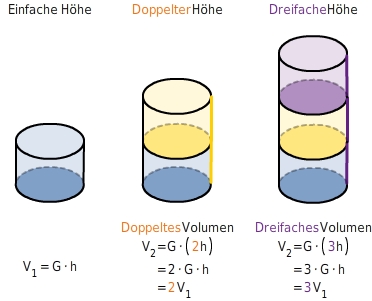
Bei gleichbleibender Grundfläche G wächst das Volumen V
zur Höhe h.
D.h., wird die Höhe mit einem Faktor k verfielfacht, vervielfacht sich das Volumen mit demselben Faktor k.

Bei gleichbleibender Höhe h wächst das Volumen V proportional zur Grundfläche G.
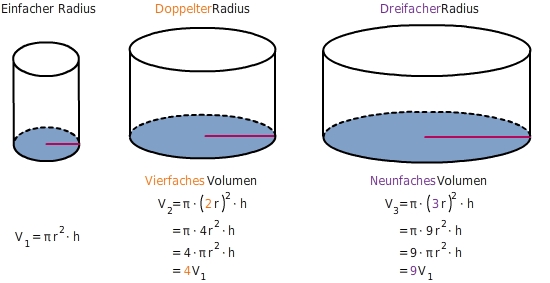
Bei gleichbleibender Höhe h wächst das Volumen V quadratisch mit dem Radius r der Grundfläche G.
D.h.: Wird der Radius mit einem Faktor k vervielfacht, vervielfacht sich das Volumen mit dem Quadrat dieses Faktors
.

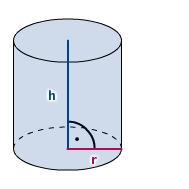
Axialschnitt und Zylinder als Rotationskörper
Wird ein Zylinder entlang der Ebene, in der die Symmetrieachse liegt, geschnitten, so entsteht der Axialschnitt des Zylinders.
Rotiert ein Rechteck um eine seiner Seiten, so entsteht als Rotationskörper ein Zylinder.Rotiert ein Rechteck um eine zur Höhe parallele Achse, so entsteht als Rotationskörper ein Hohlzylinder.

