Wertetabellen und Funktionsgraphen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, welcher Zusammenhang zwischen Wertetabellen und graphischen Darstellungen von linearen Funktionen besteht.
Wertetabellen
Eine Funktion kann auf verschiedene Arten dargestellt werden. Eine Möglichkeit ist die Wertetabelle.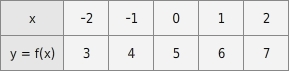 
Eine Wertetabelle hat zwei Zeilen. Die obere Zeile enthält eine Auswahl von x-Werten (Argumente der Funktion), die untere Zeile die dazu gehörenden y-Werte (Funktionswerte f(x)). Das heißt, eine Spalte einer Wertetabelle repräsentiert genau ein Wertepaar (x;y) der Funktion und damit einen Punkt (x|y) im Koordinatensystem.
Von der Wertetabelle zur graphischen Darstellung
Der Graph einer linearen Funktion ist eine Gerade. Eine Gerade ist schon durch zwei Punkte eindeutig bestimmt. Die Koordinaten dieser Punkte kannst du der Wertetabelle entnehmen und in ein passendes Koordinatensystem eintragen.
Gegeben ist die Wertetabelle einer linearen Funktion f. Zeichne den Graphen der Funktion.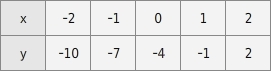 
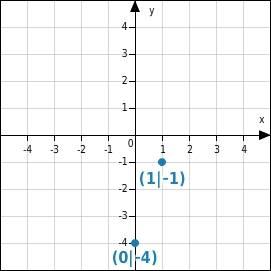
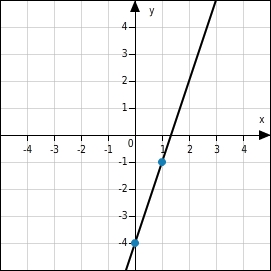
Punkte ins Koordinatensystem eintragen
Du wählst zwei Spalten der Wertetabelle so, dass sich die zugehörigen Punkte möglichst einfach im Koordinatensystem eintragen lassen. Günstig sind z.B. Punkte, deren Koordinaten ganzzahlig sind.
Gerade zeichnen
Du zeichnest durch die beiden Punkte eine Gerade. Diese Gerade ist der Graph der Funktion f und alle Punkte, deren Koordinaten in der Wertetabelle enthalten sind, liegen ebenfalls auf dieser Geraden.
Von der graphischen Darstellung zur Wertetabelle
Du kannst mit Hilfe einer graphischen Darstellung eine Wertetabelle erstellen oder eine Wertetabelle ergänzen.
Gegeben ist der Graph einer linearen Funktion. Ergänze in der Wertetabelle die fehlenden x-Koordinaten.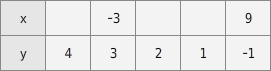 
x-Werte ergänzen
Du suchst auf der Geraden die Punkte, deren y-Koordinaten mit denen in der Wertetabelle übereinstimmen und liest an der x-Achse die dazu gehörenden x-Werte ab.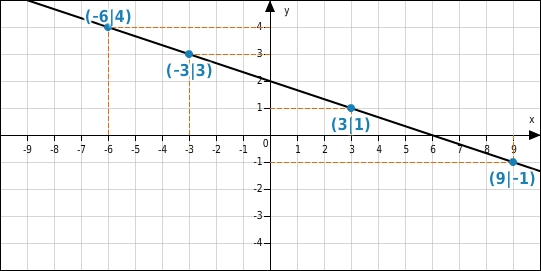 
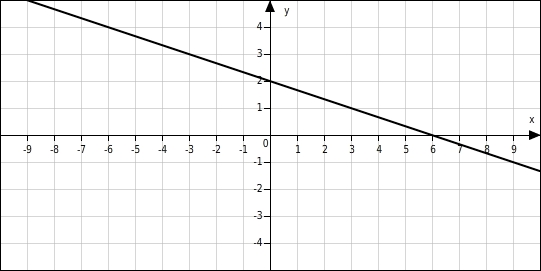
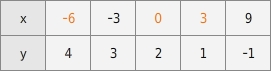
Gegeben ist der Graph einer linearen Funktion. Ergänze in der Wertetabelle die fehlenden y-Koordinaten.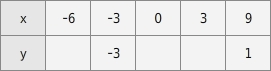 
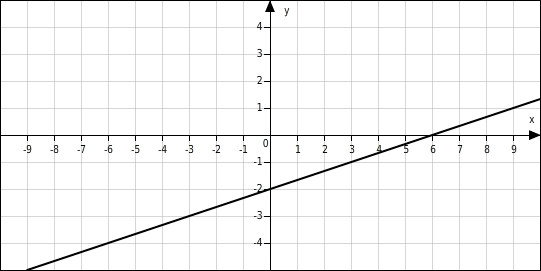
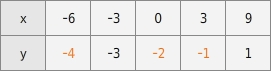
y-Werte ergänzen
Du suchst auf der Geraden die Punkte, deren x-Koordinaten mit denen in der Wertetabelle übereinstimmen und liest an der y-Achse die dazu gehörenden y-Werte ab.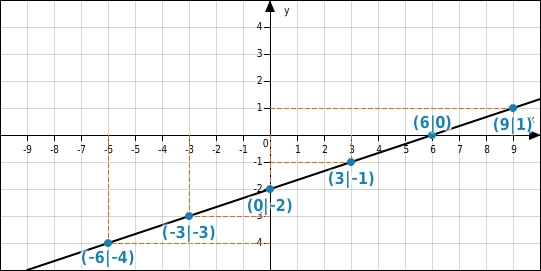 
Wertetabellen und graphische Darstellung bei Sachaufgaben
Es gibt viele Situationen im Alltag, die du mit Hilfe linearer Funktionen beschreiben kannst. Willst du zu einer Sachsituation mit linearem Zusammenhang den Graphen (die Gerade) zeichnen, überlegst du zuerst, welches Koordinatensystem geeignet ist. Wichtig sind die Beschriftung und Skalierung der Koordinatenachsen und die Wahl der Quadranten des Koordinatensystems. Um hier die richtigen Entscheidungen zu treffen, orientierst du dich am Definitions- und Wertebereich der Funktion und daran, welche Informationen du der graphischen Darstellung entnehmen möchtest.
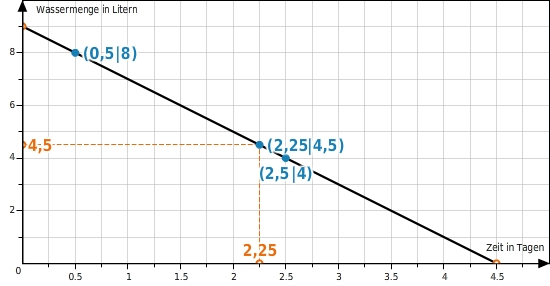
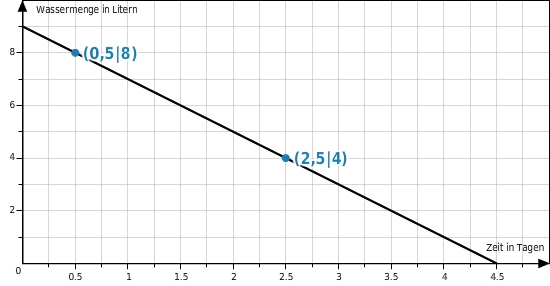
Frau Meier verreist für einige Tage. Damit ihre Pflanzen auf dem Fensterbrett nicht vertrocknen, stellt sie einen 10-l-Eimer mit Wasser daneben und verlegt zu jedem Blumentopf einen Wollfaden, der mit einem Ende im Wasser hängt und mit dem anderen Ende in der Erde steckt. 
Das Wasser läuft nun gleichmäßig vom Eimer in die Blumentöpfe. Nach einem halben Tag sind noch 8 Liter im Eimer und nach 2,5 Tagen noch 4 Liter. Wie viel Wasser hat Frau Meier in den Eimer gefüllt? Nach welcher Zeit ist der Eimer nur noch halb voll? Nach wie vielen Tagen ist der Eimer leer? 
Wertetabelle aufstellen
Du trägst alle Werte, die du dem Text entnehmen kannst, in die Tabelle ein. In der mittleren Spalte steht weder ein Wert für x noch ein Wert für y. Dort trägst du dann das Wertepaar ein, aus dem hervorgeht wann der Eimer noch halbvoll ist.
Koordinatensystem wählen
Aufgrund der Zeit- und Mengenangaben wählst du auf der x-Achse eine Skalierung in 0,5-Schritten und beschriftest die Achse mit „Zeit in Tagen“. Die y-Achse teilst du in 1-Schritten ein und beschriftest die Achse mit „Wassermenge in Litern“. Da weder die Wassermenge noch die Zeit negative Werte annehmen können, genügt der 1. Quadrant des Koordinatensystems.
Punkte ins Koordinatensystem eintragen und Geraden zeichnen
Du trägst die beiden Punkte aus der Wertetabelle ins Koordinatensystem ein und zeichnest die Gerade durch diese beiden Punkte.
Wertetabelle ergänzen
Du liest die fehlenden Koordinaten mit Hilfe der Geraden ab. Frau Meier hatte Wasser in den Eimer gefüllt. Nach Tagen ist die Hälfte der Wassermenge ( ) in die Blumentöpfe gelaufen. Nach weiteren Tagen, also nach insgesamt Tagen ist der Eimer leer. 