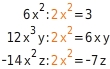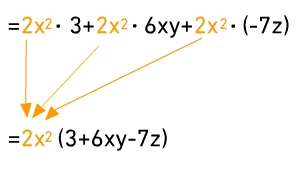bettermarks » Mathebuch » Algebra und Funktionen » Terme und Potenzen » Rechnen mit Termen und Potenzen » Multiplikation und Ausklammern bei Termen mit Potenzen

Multiplikation und Ausklammern bei Termen mit Potenzen

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?

bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.

Mehr erfahren

In diesen Erklärungen erfährst du, wie du Terme mit Potenzen mit Hilfe der Potenzgesetze multiplizieren kannst.

/wp-content/uploads/media/kem_T_TPotMul_1.jpg

Weiterhin erfährst du, wie du Terme mit Potenzen durch Ausklammern gemeinsamer Faktoren in ein Produkt umwandeln kannst.

Multiplikation von Termen mit gleichen Basen
Multiplikation von Termen mit gleichen Exponenten
Anwenden der Potenzgesetze bei Termen
Potenzieren von Potenzen
Ausklammern in Termen mit Potenzen

Multiplikation von Termen mit gleichen Basen

Wenn du Potenzen mit gleichen Basen miteinander multiplizieren möchtest, kannst du die folgende Regel verwenden:

x^{n} \cdot x^{m} = x^{n + m}

bzw.

x^{k} \cdot x^{n} \cdot x^{m} = x^{k + n + m}

Du verwendest hier das Assoziativgesetz der Multiplikation:

/wp-content/uploads/media/kem_T_TPotMul_2.jpg

x^{n}

\cdot

x^{m}

ergibt also ein Produkt, in dem der Faktor x (n + m)-mal vorkommt.

Potenzen mit gleichen Basen werden multipliziert, indem man ihre Exponenten addiert und die Basis beibehält.

Potenzen mit gleichen Exponenten werden multipliziert, indem man die Basen multipliziert und den Exponenten beibehält.

Vereinfache

x^{5}

\cdot

x^{2}

Vereinfache

/wp-content/uploads/media/kem_T_TPotMul_3.jpg

x^{5 + 2}

x^{7}

Multiplikation von Termen mit gleichen Exponenten

Wenn du Potenzen mit gleichen Exponenten miteinander multiplizieren möchtest, kannst du die folgende Regel verwenden:

x^{n} \cdot y^{n} = {(x y)}^{n}

bzw.

x^{n} \cdot y^{n} \cdot z^{n} = {(x y z)}^{n}

Du verwendest hier das Kommutativgesetz der Multiplikation:

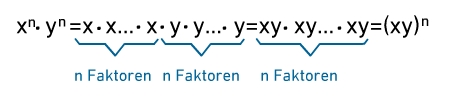
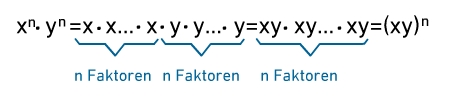
/wp-content/uploads/media/kem_T_TPotMul_4.jpg

Potenzen mit gleichen Exponenten werden multipliziert, indem man die Basen multipliziert und den Exponenten beibehält.

Vereinfache

x^{6}

\cdot

y^{6}

Vereinfache

/wp-content/uploads/media/kem_T_TPotMul_5.jpg

{(x y)}^{6}

Anwenden der Potenzgesetze bei Termen

Häufig musst du die Potenzgesetze bei der Multiplikation von Termen anwenden.

Vereinfache den Term.

2

x^{5}

\cdot

3

x^{2}

y^{3}

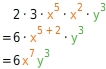
Sortieren

Alle Koeffizienten (Zahlen) sind zusammengefasst worden.Gleiche Variablen stehen jetzt nebeneinander.

2

\cdot

3

\cdot

x^{5}

\cdot

x^{2}

\cdot

y^{3}

Zusammenfassen

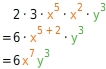
/wp-content/uploads/media/kem_T_TPotMul_6.jpg

6

x^{7}

y^{3}

Vereinfache den Term.

4

x^{7}

\cdot

2

a^{3}

\cdot

3

y^{7}

\cdot

b^{3}

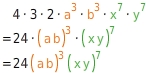
Sortieren

Alle Koeffizienten (Zahlen) sind zusammengefasst worden.Variablen mit gleichen Exponenten stehen jetzt nebeneinander.

4

\cdot

3

\cdot

2

\cdot

a^{3}

\cdot

b^{3}

\cdot

x^{7}

\cdot

y^{7}

Zusammenfassen

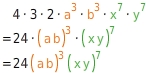
/wp-content/uploads/media/kem_T_TPotMul_7.jpg

24

{(a b)}^{3}

{(x y)}^{7}

Potenzieren von Potenzen

Du kannst Potenzen nochmals potenzieren. Du wendest dabei die folgenden Regeln an:

{(x^{n})}^{m} = x^{n \cdot m}

{(x^{n} y^{m})}^{k} = x^{n \cdot k} y^{m \cdot k}

Die Regeln gelten wieder auf Grund des Assoziativgesetzes der Multiplikation.

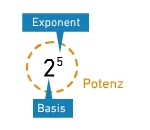
Eine Potenz wird potenziert, indem man die Exponenten multipliziert und die Basis beibehält.

Rechne aus.

{(x^{3})}^{2}

Potenzieren

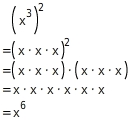
/wp-content/uploads/media/kem_T_TPotMul_8.jpg

x^{3 \cdot 2}

x^{6}

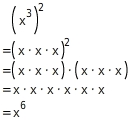
Rechne aus.

{(3 x^{3} y^{2})}^{4}

Potenzieren

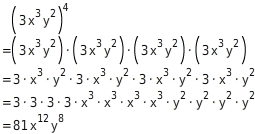
/wp-content/uploads/media/kem_T_TPotMul_9.jpg

3^{4}

\cdot

x^{3 \cdot 4}

\cdot

y^{2 \cdot 4}

81

x^{12}

y^{8}

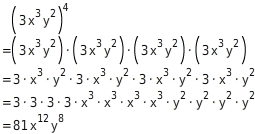
Ausklammern in Termen mit Potenzen

Du kannst Koeffizienten (Zahlen) ausklammern, einzelne Variablen oder sogar ganze Terme, die als gemeinsame Faktoren in den Summanden vorkommen.

Um einen Koeffizienten ausklammern zu können, muss dieser als Faktor (d.h. als Teiler) unter allen Koeffizienten im Term vorkommen. Du kannst also stets den größten gemeinsamen Teiler (ggT) aller Koeffizienten ausklammern.

Klammere den größtmöglichen Faktor aus.

9

x

+

12

y

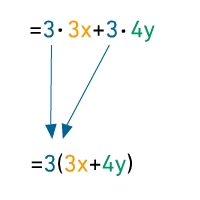
Ausklammern

Der größte gemeinsame Teiler von 9 und 12 ist 3.

9 x : 3 = 3 x

12 y : 3 = 4 y

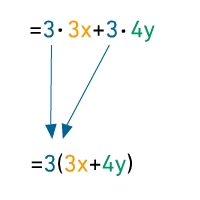
/wp-content/uploads/media/kem_T_TPotMul_10.jpg

Klammere so weit aus wie möglich.

4

x^{2}

+

12

x

y

-

10

y

z^{2}

+

2

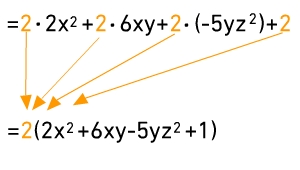
Ausklammern

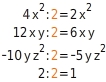
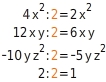
Du kannst auch bei mehr als zwei Summanden ausklammern. Hier wurde bei allen vier Summanden der Faktor 2 ausgeklammert.Du erhältst die Terme in der Klammer, indem du jeden einzelnen Summanden des ursprünglichen Ausdrucks durch 2 dividierst. /wp-content/uploads/media/kem_T_TPotMul_11.jpg

/wp-content/uploads/media/kem_T_TPotMul_11.jpg

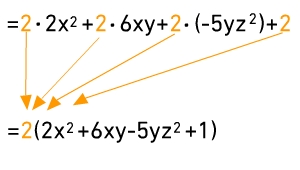
/wp-content/uploads/media/kem_T_TPotMul_12.jpg

Du kannst Koeffizienten und Variablen zusammen ausklammern, wenn der ausgeklammerte Term ein Teiler aller Summanden des ursprünglichen Terms ist.

Klammere so weit aus wie möglich.

3

x^{2}

-

6

x

y

Ausklammern

3

x^{2}

und -6xy enthalten beide die Faktoren 3 und x. Diese kannst du ausklammern.

3

x

x - 2 y

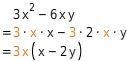
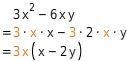
Klammere so weit aus wie möglich.

6

x^{2}

+

12

x^{3}

y

-

14

x^{2}

z

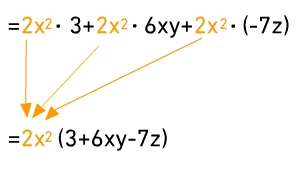
Ausklammern

Hier wurde bei allen vier Summanden der Faktor

2

x^{2}

ausgeklammert. /wp-content/uploads/media/kem_T_TPotMul_14.jpg

/wp-content/uploads/media/kem_T_TPotMul_15.jpg

Multiplikation und Ausklammern bei Termen mit Potenzen

Multiplikation von Termen mit gleichen Basen

Multiplikation von Termen mit gleichen Exponenten

Anwenden der Potenzgesetze bei Termen

Potenzieren von Potenzen

Ausklammern in Termen mit Potenzen

Produkte

Unternehmen

Service