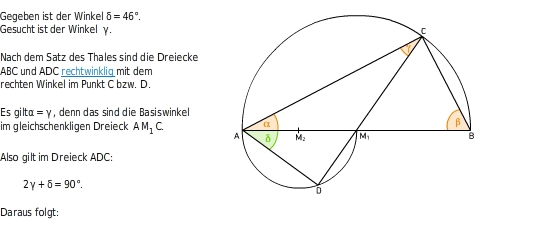
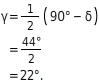Satz des Thales
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenDer Satz des Thales
Der nach dem griechischen Mathematiker und Philosophen Thales von Milet (~ 625 v.Chr. - ~ 547 v.Chr.) benannte Satz des Thales besagt:
Wenn der Punkt C auf dem
mit dem
liegt, dann hat das
ABC bei C einen
.
Der Kreis mit dem Durchmesser
heißt daher auch Thaleskreis dieser Strecke.
Die Umkehrung des Satzes gilt ebenfalls:
In einem
ABC mit dem rechtem Winkel im Punkt C liegt der Punkt C auf dem Kreis mit demDurchmesser
.
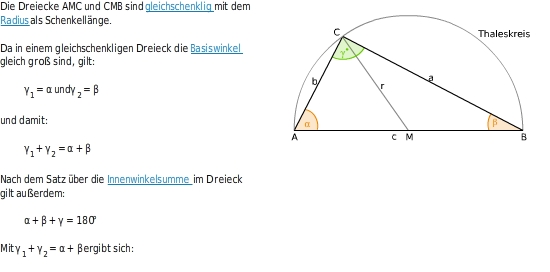
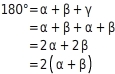Nach Division durch 2 erhältst du:
Konstruktionen mit dem Satz des Thales
Du kannst den Satz des Thales nutzen, um ein
zu konstruieren.
Rechtwinkliges Dreieck ABC mit dem rechten Winkel im Punkt C
Du beginnst mit der Seite, die dem rechten Winkel gegenüberliegt, also der Seite
mit der Länge c.
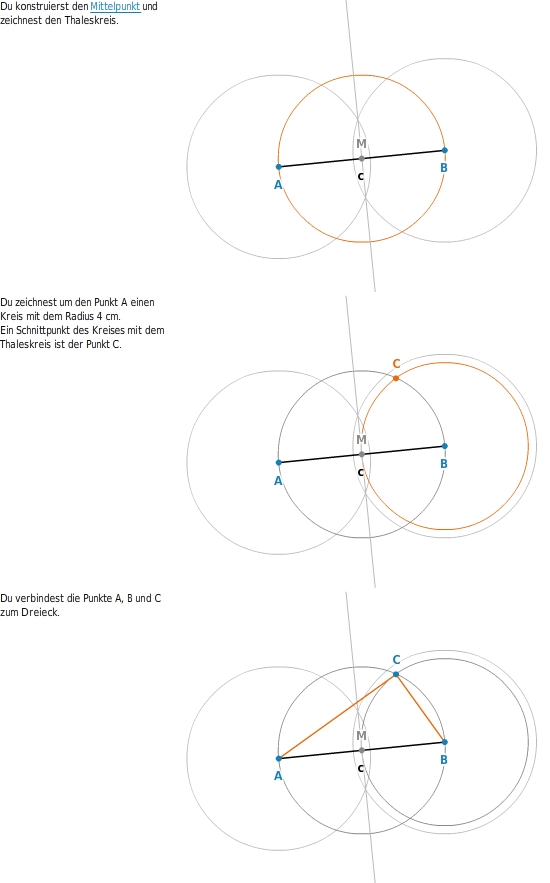
Hast du statt der Seitenlänge a den
gegeben, trägst du im Punkt B den Winkel an.
Der Schnittpunkt des Schenkels mit dem Thaleskreis ist der Punkt C.
Winkelberechnungen mit dem Satz des Thales
Sind die Voraussetzungen aus dem Satz des Thales erfüllt, kannst du mit seiner Hilfe die Größe von
berechnen.
