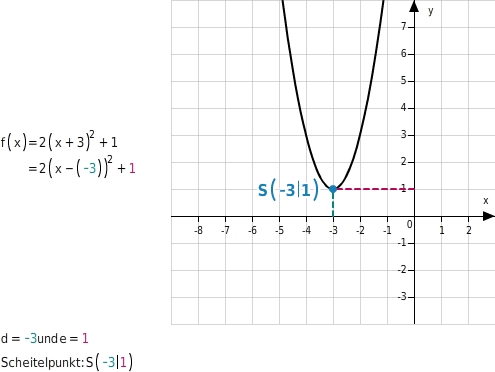
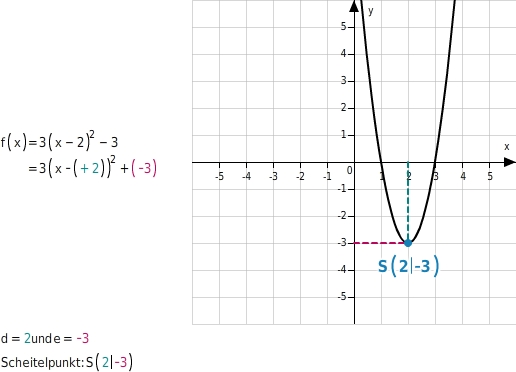
Quadratische Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenFunktionsterm und Graph einer quadratischen Funktion
Funktionen, die sich mit Termen der Form
mit
≠
darstellen lassen, heißen quadratische Funktionen.
Ihre Graphen heißen Parabeln.
Die Gleichung
heißt Parabelgleichung.
Alle Punkte x | y , deren Koordinaten x und y diese Gleichung erfüllen, liegen somit auf der Parabel.
Die einfachste quadratische Funktion hat die Gleichung
.
Ihr Graph ist die Normalparabel.
 Du berechnest den Funktionswert (y-Wert) zu einem Argument (x-Wert), indem du dieses in den Funktionsterm einsetzt.
Du berechnest den Funktionswert (y-Wert) zu einem Argument (x-Wert), indem du dieses in den Funktionsterm einsetzt.
 Du berechnest den Funktionswert (y-Wert) zu einem Argument (x-Wert), indem du dieses in den Funktionsterm einsetzt.
Du berechnest den Funktionswert (y-Wert) zu einem Argument (x-Wert), indem du dieses in den Funktionsterm einsetzt.
Besondere Punkte von quadratischen Funktionen
Nullstelle y-Achsenabschnitt
y-Achsenabschnitt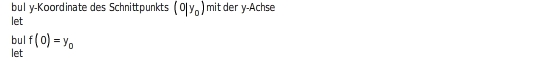
 Scheitelpunkt:Ist die Parabel nach unten geöffnet, dann ist der Scheitelpunkt gleich dem Hochpunkt (
).Ist die Parabel nach oben geöffnet, dann ist der Scheitelpunkt gleich dem Tiefpunkt (
).
Ist die Lage des Scheitelpunktes bekannt, kann die Parabel, sofern sie nicht durch
verzerrt ist, mit Hilfe einer Parabelschablone schnell in ein
gezeichnet werden.
Scheitelpunkt:Ist die Parabel nach unten geöffnet, dann ist der Scheitelpunkt gleich dem Hochpunkt (
).Ist die Parabel nach oben geöffnet, dann ist der Scheitelpunkt gleich dem Tiefpunkt (
).
Ist die Lage des Scheitelpunktes bekannt, kann die Parabel, sofern sie nicht durch
verzerrt ist, mit Hilfe einer Parabelschablone schnell in ein
gezeichnet werden.
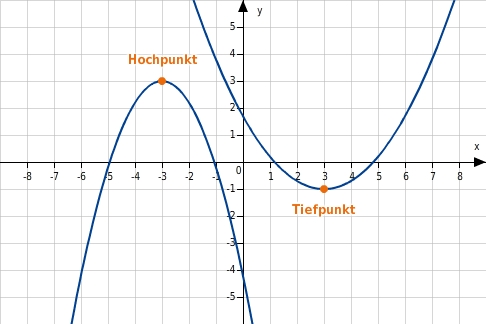
 y-Achsenabschnitt
y-Achsenabschnitt
 Scheitelpunkt:Ist die Parabel nach unten geöffnet, dann ist der Scheitelpunkt gleich dem Hochpunkt (
).Ist die Parabel nach oben geöffnet, dann ist der Scheitelpunkt gleich dem Tiefpunkt (
).
Ist die Lage des Scheitelpunktes bekannt, kann die Parabel, sofern sie nicht durch
verzerrt ist, mit Hilfe einer Parabelschablone schnell in ein
gezeichnet werden.
Scheitelpunkt:Ist die Parabel nach unten geöffnet, dann ist der Scheitelpunkt gleich dem Hochpunkt (
).Ist die Parabel nach oben geöffnet, dann ist der Scheitelpunkt gleich dem Tiefpunkt (
).
Ist die Lage des Scheitelpunktes bekannt, kann die Parabel, sofern sie nicht durch
verzerrt ist, mit Hilfe einer Parabelschablone schnell in ein
gezeichnet werden.

Verschiebung entlang der y-Achse
Addierst du zum Funktionsterm der Funktion f mit
eine Konstante e, dann ist der Graph der neuen Funktion
eine entlang der y-Achse verschobene Normalparabel.
Der Scheitelpunkt dieser Parabel ist
.
Für
wird die Parabel entlang der y-Achse um e Einheiten nach oben verschoben.
Für
wird die Parabel entlang der y-Achse um e Einheiten nach unten verschoben.


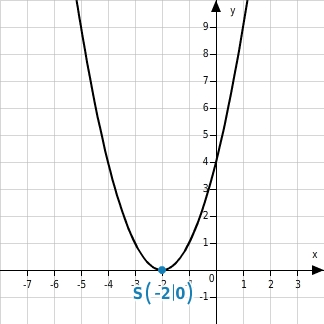
Verschiebung entlang der x-Achse
Subtrahierst du von den Argumenten der Funktion f mit
eine Konstante d, dann ist der Graph der neuen Funktion
eine entlang der x-Achse verschobene Normalparabel.
Der Scheitelpunkt dieser Parabel ist
.
Für
ist die Parabel entlang der x-Achse um d Einheiten nach rechts verschoben.
Für
ist die Parabel entlang der x-Achse um d Einheiten nach links verschoben.

=

Scheitelpunktform
Oft werden quadratische Funktionsterme in der Scheitelpunktform angegeben:
Du kannst aus ihr die Koordinaten des Scheitelpunkts der zugehörigen Parabel direkt ablesen:
Zusätzlich kannst du den Streckfaktor
der Parabel ablesen. Es ist der Faktor vor der Klammer.