Mit der abc-Formel quadratische Gleichungen lösen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHerleitung der abc-Formel
Lösungsformel für eine quadratische Gleichung in allgemeiner Form
abc-Formel:
Die abc-Formel entsteht aus der quadratischen Gleichung in allgemeiner Form
(
≠
) durch
.


Anzahl der Lösungen mit der Diskriminante bestimmen
Diskriminante D zur abc-Formel:
Betrachtest du die Diskriminante D der
, kannst du angeben, wie viele Lösungen eine
hat.
D > 0,
die Gleichung hat zwei Lösungen.
D = 0,
die Gleichung hat eine Lösung.
die Gleichung hat keine Lösung.
Lösen quadratischer Gleichungen
Lösungsformel für eine quadratische Gleichung in allgemeiner Form
abc-Formel:
Du berechnest mit
,
und
die Diskriminante
und setzt dann in die abc-Formel ein:
Die Gleichung hat also zwei Lösungen.

 und
und 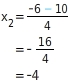

 und
und