Grundlagen zu Potenzfunktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, was eine Potenzfunktion ist, und lernst die wichtigsten Grundlagen zu Potenzfunktion mit natürlichen Exponenten kennen.
Was ist eine Potenzfunktion?
Eine Potenzfunktion (mit natürlichem Exponenten) ist eine Funktion mit einem Funktionsterm der Form . Die natürliche Zahl ist der Grad der Potenzfunktion, man spricht auch von einer Potenzfunktion vom Grad . Eine allgemeine Potenzfunktion hat einen Funktionsterm der Form . Der Koeffizient ist eine reelle Zahl ungleich Null.
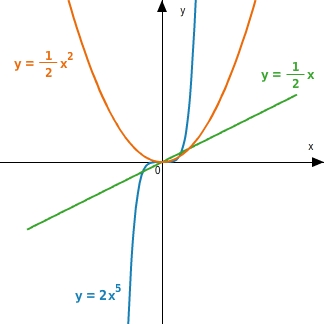
Charakteristische Graphen von Potenzfunktionen
Abhängig von der des Exponenten und vom Koeffizienten gibt es vier charakteristische Graphen von allgemeinen Potenzfunktionen. Die Graphen von Potenzfunktionen weisen stets eine der folgenden Symmetrien auf: 
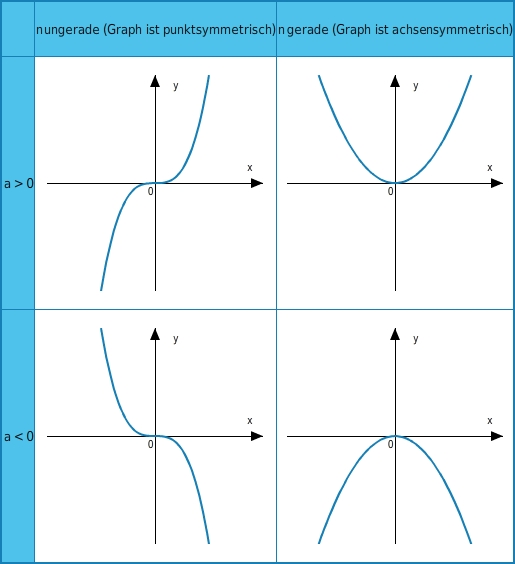Der einer allgemeinen Potenzfunktion ist die Menge ℝ der reellen Zahlen. Der kleinstmögliche hängt ab vom Grad , und vom des Koeffizienten : 
Bedeutung des Koeffizienten im Term von Potenzfunktionen
Der a einer bewirkt im Vergleich zu eine 
