Grundbegriffe der Wahrscheinlichkeitsrechnung
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier lernst du die Grundbegriffe der Wahrscheinlichkeitsrechnung wie Zufallsexperiment, Ergebnis und Ereignis kennen. Außerdem erfährst du hier, wie du mögliche Ergebnisse von Zufallsexperimenten mit Hilfe von Baumdiagrammen darstellen kannst.
Erkennen von Zufallsexperimenten
Ein Zufallsexperiment ist ein Vorgang, der mehr als einen möglichen Ausgang (ein sogenanntes Ergebnis) haben kann. Dabei kann aber nicht vorausgesagt werden, welches Ergebnis das Zufallsexperiment haben wird.
Münzwurf
 Das Werfen einer Münze ist ein Zufallsexperiment, da sowohl Kopf als auch Zahl erscheinen können. Es kann jedoch nicht vorhergesagt werden, ob Kopf oder Zahl erscheinen wird.
Das Werfen einer Münze ist ein Zufallsexperiment, da sowohl Kopf als auch Zahl erscheinen können. Es kann jedoch nicht vorhergesagt werden, ob Kopf oder Zahl erscheinen wird.
 Das Werfen einer Münze ist ein Zufallsexperiment, da sowohl Kopf als auch Zahl erscheinen können. Es kann jedoch nicht vorhergesagt werden, ob Kopf oder Zahl erscheinen wird.
Das Werfen einer Münze ist ein Zufallsexperiment, da sowohl Kopf als auch Zahl erscheinen können. Es kann jedoch nicht vorhergesagt werden, ob Kopf oder Zahl erscheinen wird.
Würfeln
 Das Werfen eines mit den Augenzahlen 1, 2, 3, 4, 5 und 6 beschrifteten Würfels ist ein Zufallsexperiment, da jede der genannten Ziffern als Ergebnis erscheinen kann. Es kann jedoch nicht vorhergesagt werden, welche der sechs Ziffern erscheinen wird.
Das Werfen eines mit den Augenzahlen 1, 2, 3, 4, 5 und 6 beschrifteten Würfels ist ein Zufallsexperiment, da jede der genannten Ziffern als Ergebnis erscheinen kann. Es kann jedoch nicht vorhergesagt werden, welche der sechs Ziffern erscheinen wird.
 Das Werfen eines mit den Augenzahlen 1, 2, 3, 4, 5 und 6 beschrifteten Würfels ist ein Zufallsexperiment, da jede der genannten Ziffern als Ergebnis erscheinen kann. Es kann jedoch nicht vorhergesagt werden, welche der sechs Ziffern erscheinen wird.
Das Werfen eines mit den Augenzahlen 1, 2, 3, 4, 5 und 6 beschrifteten Würfels ist ein Zufallsexperiment, da jede der genannten Ziffern als Ergebnis erscheinen kann. Es kann jedoch nicht vorhergesagt werden, welche der sechs Ziffern erscheinen wird.
Zufallsexperimente erkennen
Welche der folgenden Vorgänge sind Zufallsexperimente bzw. welche der beschriebenen Ereignisse sind zufällig?

Zufall erkennen
Es kann nicht vorhergesagt werden, welche der 32 Karten nach dem Mischen die dreizehnte Karte von oben ist. Es handelt sich also um ein Zufallsexperiment.
Jede gewürfelte Augenzahl ist entweder gerade ({2; 4; 6}) oder ungerade ({1; 3; 5}). Somit ist das Werfen einer geraden oder ungeraden Zahl kein zufälliges Ereignis, es tritt in jedem Fall ein.
Auch wenn eine Münze 10-mal geworfen wurde und jedes Mal „Kopf“ erschien, kann beim nächsten Münzwurf entweder „Kopf“ oder „Zahl“ erscheinen und nicht notwendigerweise „Zahl“. Es handelt sich also um ein Zufallsexperiment.
Die Innenwinkelsumme ist in JEDEM Dreieck gleich 180°. Somit ist das Bestimmen der Innenwinkelsumme in einem zufällig gewählten Dreieck kein Zufallsexperiment.

Ergebnis - Ereignis - Ergebnismenge
Die möglichen Ausgänge eines Zufallsexperimentes nennt man Ergebnisse.
Wenn man alle möglichen Ergebnisse eines Zufallsexperimentes in einer Menge zusammenfasst, erhält man die Ergebnismenge. Sie wird üblicherweise mit dem Symbol Ω (sprich Omega) bezeichnet.
Jede Zusammenfassung von einem oder mehreren Ergebnissen eines Zufallsexperimentes in einer Menge nennt man Ereignis.
Es gibt außerdem noch das sogenannte „unmögliche Ereignis“, das keinerlei Ergebnis enthält. Dies wird im folgenden Abschnitt behandelt.
Ergebnisse, Ereignisse und Ergebnismenge beim Würfel
 Das Werfen eines Würfels ist ein Zufallsexperiment.
Jede der möglichen Augenzahlen 1, 2, 3, 4, 5 und 6 ist ein Ergebnis.
Die Ergebnismenge ist die Zusammenfassung aller möglichen Ergebnisse in einer Menge. Beim Würfeln ist also Ω= {1; 2; 3; 4; 5; 6} die Ergebnismenge.
Ein mögliches Ereignis ist zum Beispiel „Würfel zeigt eine gerade Zahl“ und wird durch die Menge {2; 4; 6} dargestellt.
Das Werfen eines Würfels ist ein Zufallsexperiment.
Jede der möglichen Augenzahlen 1, 2, 3, 4, 5 und 6 ist ein Ergebnis.
Die Ergebnismenge ist die Zusammenfassung aller möglichen Ergebnisse in einer Menge. Beim Würfeln ist also Ω= {1; 2; 3; 4; 5; 6} die Ergebnismenge.
Ein mögliches Ereignis ist zum Beispiel „Würfel zeigt eine gerade Zahl“ und wird durch die Menge {2; 4; 6} dargestellt.
 Das Werfen eines Würfels ist ein Zufallsexperiment.
Jede der möglichen Augenzahlen 1, 2, 3, 4, 5 und 6 ist ein Ergebnis.
Die Ergebnismenge ist die Zusammenfassung aller möglichen Ergebnisse in einer Menge. Beim Würfeln ist also Ω= {1; 2; 3; 4; 5; 6} die Ergebnismenge.
Ein mögliches Ereignis ist zum Beispiel „Würfel zeigt eine gerade Zahl“ und wird durch die Menge {2; 4; 6} dargestellt.
Das Werfen eines Würfels ist ein Zufallsexperiment.
Jede der möglichen Augenzahlen 1, 2, 3, 4, 5 und 6 ist ein Ergebnis.
Die Ergebnismenge ist die Zusammenfassung aller möglichen Ergebnisse in einer Menge. Beim Würfeln ist also Ω= {1; 2; 3; 4; 5; 6} die Ergebnismenge.
Ein mögliches Ereignis ist zum Beispiel „Würfel zeigt eine gerade Zahl“ und wird durch die Menge {2; 4; 6} dargestellt.
Die Ergebnisse eines Zufallsexperimentes
Was ist ein mögliches Ergebnis beim einmaligen Werfen eines Würfels mit dem abgebildeten Würfelnetz?
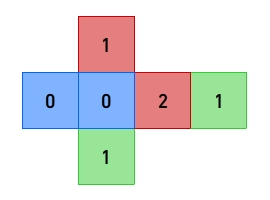


Ergebnisse zuordnen
Du kannst die Farben oder die Ziffern oder Kombinationen aus Farben und Ziffern als mögliche Ergebnisse betrachten.
Wenn du die Farben als Ergebnisse betrachtest, sind Grün, Rot und Blau mögliche Ergebnisse.
Wenn du die Ziffern als Ergebnisse betrachtest, sind 0, 1 und 2 mögliche Ergebnisse.
Wenn du die Kombinationen aus Ziffern und Farben als Ergebnisse betrachtest, sind (Blau; 0), (Rot; 1), (Rot; 2) und (Grün; 1) mögliche Ergebnisse.
Beachte, dass zum Beispiel {0; 1; 2}, {Rot; Grün} oder {(Rot; 1)} Zusammenfassungen von einem bzw. mehreren Ergebnissen zu Mengen und somit Ereignisse sind.Dabei spielt es keine Rolle, ob in solch einer Zusammenfassung nur ein einziges Ergebnis enthalten ist.

Die Ergebnismenge beim Münzwurf
Beim Münzwurf können die Ergebnisse Kopf (K) oder Zahl (Z) erscheinen. Somit ist die Ergebnismenge Ω = {K; Z}.


Welche der angegebenen Mengen ist eine Ergebnismenge für das Ziehen einer Kugel aus der abgebildeten Urne?
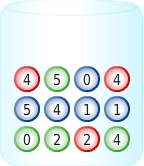


Ergebnismenge zuordnen
Die Ergebnismenge besteht aus allen möglichen Ergebnissen des Zufallsexperimentes „Ziehen einer Kugel aus der abgebildeten Urne‟.
Du kannst die Farben oder die Ziffern als mögliche Ergebnisse betrachten.
Wenn du die Ziffern als Ergebnisse betrachtest, ist die Ergebnismenge Ω = {0; 1; 2; 4; 5}.Wenn du die Farben als Ergebnisse betrachtest, ist die Ergebnismenge Ω = {Rot; Grün; Blau}.
Beide Mengen kommen in der Auswahl vor.

Ereignisse beim Würfeln
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Das Ereignis E - „Eine Zahl kleiner als 3 wird gewürfelt ‟ - besteht aus den Ergebnissen 1 und 2. üblicherweise schreibt man ein solches Ereignis als Menge:
E = {1; 2}.
Jede Zusammenfassung von einem oder mehreren Ergebnissen eines Zufallsexperimentes in einer Menge nennt man Ereignis.
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Bestimme die zum gegebenen Ereignis E gehörigen Ergebnisse.
E ist das Ereignis „Eine ungerade Zahl wird gewürfelt ‟.
Ziehe die zum Ereignis gehörigen Ergebnisse in den markierten Bereich.




Ereignis bestimmen
Alle ungeraden Augenzahlen sind Ergebnisse, die zum Ereignis „Eine ungerade Zahl wird gewürfelt ‟ gehören.Du ziehst also 1, 3 und 5 in den markierten Bereich.

Sichere und unmögliche Ereignisse sowie Gegenereignisse
Zu jedem Ereignis E eines Zufallsexperimentes gibt es das sogenannte Gegenereignis
. Es besteht aus all denjenigen möglichen Ergebnissen des Zufallsexperimentes, die nicht zu E gehören.
Die Ergebnismenge Ω ist die Zusammenfassung aller möglichen Ergebnisse eines Zufallsexperimentes. Sie ist somit ebenfalls ein Ereignis. Da dieses Ereignis immer eintritt, nennt man dieses Ereignis auch sicheres Ereignis.
Das Gegenereignis zum sicheren Ereignis zeichnet sich durch die Abwesenheit möglicher Ergebnisse eines Zufallsexperimentes aus. Es ist also die leere Menge und wird mit ∅ bzw. { } bezeichnet. Man nennt ∅ bzw. { } das unmögliche Ereignis.
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Weiterhin sei E das Ereignis „Eine Zahl größer oder gleich 3 wird gewürfelt“.
Das heißt, es ist E = {3; 4; 5; 6}.
Dann besteht das zu E gehörige Gegenereignis
aus denjenigen Augenzahlen, die nicht zu E gehören. Somit gilt
= {1; 2}.
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Bestimme das Gegenereignis
zum gegebenen Ereignis E „Keine 4 wird gewürfelt“.








Gegenereignis bestimmen
Du wählst alle diejenigen Ergebnisse der Ergebnismenge aus, die nicht zu E gehören.Dies ist aber nur ein Ergebnis, und zwar das Ergebnis 4.

Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Weiterhin sei E das Ereignis „Eine positive Zahl wird gewürfelt ‟. Dann ist E das sichere Ereignis, denn jede würfelbare Augenzahl ist positiv.Das heißt, es ist E = {1; 2; 3; 4; 5; 6} = Ω.
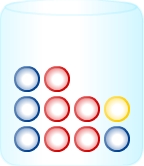 Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Mindestens eine der Kugeln ist rot oder blau ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Mindestens eine der Kugeln ist rot oder blau ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Ereignisart bestimmen
Das Ereignis ist sicher, da die gelbe Kugel nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden.
Somit muss bei zwei gezogenen Kugeln immer eine dabei sein, die nicht gelb, also rot oder blau ist.

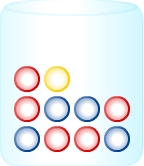 Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Beide Kugeln sind gelb ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Beide Kugeln sind gelb ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Ereignisart bestimmen
Das Ereignis ist unmöglich, da die gelbe Kugel nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden.

Mehrstufige Zufallsexperimente und Baumdiagramme
Wenn mehrere Zufallsexperimente nacheinander durchgeführt werden, spricht man von einem mehrstufigen Zufallsexperiment. Zwei- bzw. dreistufige Zufallsexperimente können sehr gut mit Hilfe von Baumdiagrammen (kurz: Bäumen) dargestellt werden, sofern die einzelnen Teilexperimente nicht zu viele Ergebnisse haben.
Der Aufbau eines Baumdiagramms, das zu einem mehrstufigen Zufallsexperiment gehört, wird hier anhand einiger Beispiele erklärt:
Zweifacher Münzwurf
Beim zweifachen Münzwurf können bei jedem Teilexperiment die Ergebnisse Kopf (K) oder Zahl (Z) erscheinen.
Ein Baumdiagramm hat immer einen Startknoten. Dieser Startknoten wird auch Wurzel bzw. Wurzelknoten des Baumdiagramms genannt. Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Werfen einer Münze ‟ entsprechen:K und Z. 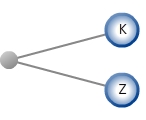 In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Werfen einer Münze“ führen:K und Z.
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel:
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Werfen einer Münze“ führen:K und Z.
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel: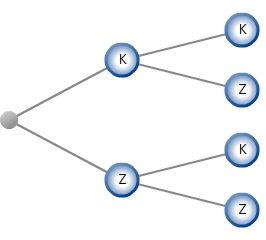
 In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Werfen einer Münze“ führen:K und Z.
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel:
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Werfen einer Münze“ führen:K und Z.
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel:
Ein anderer möglicher Baum ist zum Beispiel dieser: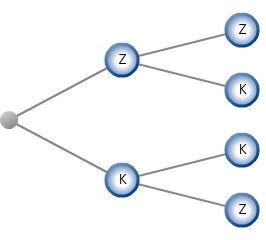 Endknoten bzw. Blätter eines Baumdiagramms heißen diejenigen Knoten, die die möglichen Ergebnisse des letzten Teilexperimentes eines mehrstufigen Zufallsexperimentes darstellen.
Zu jedem Endknoten führt vom Startknoten ausgehend eine Kette von Zweigen - ein sogenannter Pfad.
Jeder Pfad entspricht einem möglichen Ergebnis des mehrstufigen Zufallsexperimentes.
Oft schreibt man daher neben jedem Endknoten das zum Pfad gehörige Ergebnis. Bei weitergehenden Berechnungen trägt man oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das zweimalige Werfen einer Münze einschließlich aller Ergebnisse wie folgt aus:
Endknoten bzw. Blätter eines Baumdiagramms heißen diejenigen Knoten, die die möglichen Ergebnisse des letzten Teilexperimentes eines mehrstufigen Zufallsexperimentes darstellen.
Zu jedem Endknoten führt vom Startknoten ausgehend eine Kette von Zweigen - ein sogenannter Pfad.
Jeder Pfad entspricht einem möglichen Ergebnis des mehrstufigen Zufallsexperimentes.
Oft schreibt man daher neben jedem Endknoten das zum Pfad gehörige Ergebnis. Bei weitergehenden Berechnungen trägt man oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das zweimalige Werfen einer Münze einschließlich aller Ergebnisse wie folgt aus: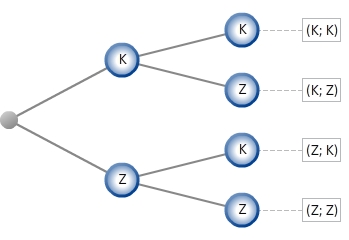 Beachte hierbei auch die Schreibweise der Ergebnisse als geordnete Paare. Oft schreibt man die Ergebnisse auch einfach als Verkettung von geeigneten Buchstaben wie zum Beispiel „ZK ‟ für „Erster Wurf zeigt Zahl - zweiter Wurf zeigt Kopf ‟.
Wenn man sich nur für die zum Ereignis E „Es erscheint Kopf genau einmal ‟ gehörigen Ergebnisse interessiert, sieht das Baumdiagramm wie folgt aus:
Beachte hierbei auch die Schreibweise der Ergebnisse als geordnete Paare. Oft schreibt man die Ergebnisse auch einfach als Verkettung von geeigneten Buchstaben wie zum Beispiel „ZK ‟ für „Erster Wurf zeigt Zahl - zweiter Wurf zeigt Kopf ‟.
Wenn man sich nur für die zum Ereignis E „Es erscheint Kopf genau einmal ‟ gehörigen Ergebnisse interessiert, sieht das Baumdiagramm wie folgt aus: 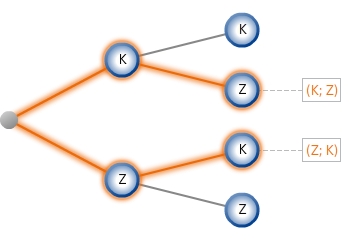
 Endknoten bzw. Blätter eines Baumdiagramms heißen diejenigen Knoten, die die möglichen Ergebnisse des letzten Teilexperimentes eines mehrstufigen Zufallsexperimentes darstellen.
Zu jedem Endknoten führt vom Startknoten ausgehend eine Kette von Zweigen - ein sogenannter Pfad.
Jeder Pfad entspricht einem möglichen Ergebnis des mehrstufigen Zufallsexperimentes.
Oft schreibt man daher neben jedem Endknoten das zum Pfad gehörige Ergebnis. Bei weitergehenden Berechnungen trägt man oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das zweimalige Werfen einer Münze einschließlich aller Ergebnisse wie folgt aus:
Endknoten bzw. Blätter eines Baumdiagramms heißen diejenigen Knoten, die die möglichen Ergebnisse des letzten Teilexperimentes eines mehrstufigen Zufallsexperimentes darstellen.
Zu jedem Endknoten führt vom Startknoten ausgehend eine Kette von Zweigen - ein sogenannter Pfad.
Jeder Pfad entspricht einem möglichen Ergebnis des mehrstufigen Zufallsexperimentes.
Oft schreibt man daher neben jedem Endknoten das zum Pfad gehörige Ergebnis. Bei weitergehenden Berechnungen trägt man oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das zweimalige Werfen einer Münze einschließlich aller Ergebnisse wie folgt aus: Beachte hierbei auch die Schreibweise der Ergebnisse als geordnete Paare. Oft schreibt man die Ergebnisse auch einfach als Verkettung von geeigneten Buchstaben wie zum Beispiel „ZK ‟ für „Erster Wurf zeigt Zahl - zweiter Wurf zeigt Kopf ‟.
Wenn man sich nur für die zum Ereignis E „Es erscheint Kopf genau einmal ‟ gehörigen Ergebnisse interessiert, sieht das Baumdiagramm wie folgt aus:
Beachte hierbei auch die Schreibweise der Ergebnisse als geordnete Paare. Oft schreibt man die Ergebnisse auch einfach als Verkettung von geeigneten Buchstaben wie zum Beispiel „ZK ‟ für „Erster Wurf zeigt Zahl - zweiter Wurf zeigt Kopf ‟.
Wenn man sich nur für die zum Ereignis E „Es erscheint Kopf genau einmal ‟ gehörigen Ergebnisse interessiert, sieht das Baumdiagramm wie folgt aus: 
Zwei Glücksräder
Die beiden abgebildeten Glücksräder werden jeweils einmal gedreht. Zuerst wird das linke, dann das rechte Glücksrad gedreht. Die Farben werden in der Reihenfolge der Drehungen notiert.
 Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad ‟ entsprechen:
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad ‟ entsprechen: und
und  .
. In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad ‟ führen:
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad ‟ führen: und
und  .
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel
.
Die Reihenfolge der Zweige bzw. Knoten spielt dabei keine Rolle.Es gibt also mehrere korrekte Baumdiagramme, die das Zufallsexperiment beschreiben.Ein möglicher Baum ist zum Beispiel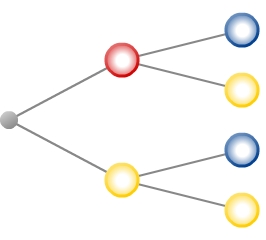

 Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad ‟ entsprechen:
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad ‟ entsprechen: In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad ‟ führen:
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad ‟ führen:
Ein weiteres korrektes Baumdiagramm ist folgendes: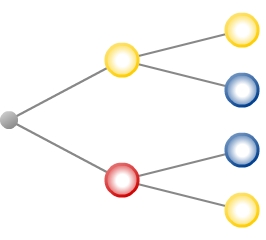 Wiederum kann neben den Endknoten des Baumdiagramms das zum jeweiligen Pfad gehörige Ergebnis des mehrstufigen Zufallsexperimentes ergänzt werden.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das Drehen am linken Glücksrad mit darauffolgendem Drehen am rechten Glücksrad einschließlich aller Ergebnisse wie folgt aus:
Wiederum kann neben den Endknoten des Baumdiagramms das zum jeweiligen Pfad gehörige Ergebnis des mehrstufigen Zufallsexperimentes ergänzt werden.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das Drehen am linken Glücksrad mit darauffolgendem Drehen am rechten Glücksrad einschließlich aller Ergebnisse wie folgt aus: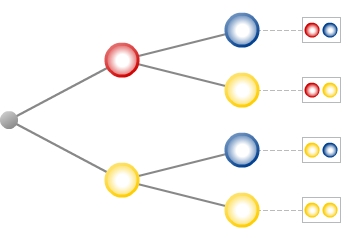
 Wiederum kann neben den Endknoten des Baumdiagramms das zum jeweiligen Pfad gehörige Ergebnis des mehrstufigen Zufallsexperimentes ergänzt werden.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das Drehen am linken Glücksrad mit darauffolgendem Drehen am rechten Glücksrad einschließlich aller Ergebnisse wie folgt aus:
Wiederum kann neben den Endknoten des Baumdiagramms das zum jeweiligen Pfad gehörige Ergebnis des mehrstufigen Zufallsexperimentes ergänzt werden.
In unserem Beispiel sieht ein vollständiges Baumdiagramm für das Drehen am linken Glücksrad mit darauffolgendem Drehen am rechten Glücksrad einschließlich aller Ergebnisse wie folgt aus:
Statt die Knoten und Ergebnisse entsprechend zu färben, kann man zum Beispiel auch die Anfangsbuchstaben der Farben als Markierungen der Knoten und Ergebnisse wählen. In unserem Fall (R - Rot, G - Gelb, B - Blau) würde ein zugehöriges Baumdiagramm so aussehen: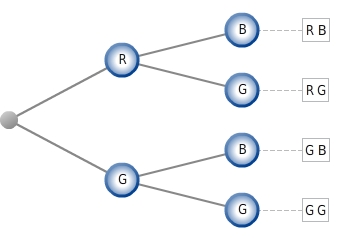 Beachte hierbei auch die Schreibweise der Ergebnisse als Verkettungen der Anfangsbuchstaben der Farben. Man hätte die Ergebnisse auch als geordnete Paare der Anfangsbuchstaben der Farben angeben können. (R; G) wäre dann das Ergebnis „Linkes Glücksrad bleibt auf Rot stehen - Rechtes Glücksrad bleibt auf Gelb stehen.“
Wiederum trägt man bei weitergehenden Berechnungen oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
Wenn man sich nur für die zum Ereignis E „Es erscheint die Farbe Gelb genau einmal ‟ gehörigen Ergebnisse interessiert, sähe das Baumdiagramm wie folgt aus:
Beachte hierbei auch die Schreibweise der Ergebnisse als Verkettungen der Anfangsbuchstaben der Farben. Man hätte die Ergebnisse auch als geordnete Paare der Anfangsbuchstaben der Farben angeben können. (R; G) wäre dann das Ergebnis „Linkes Glücksrad bleibt auf Rot stehen - Rechtes Glücksrad bleibt auf Gelb stehen.“
Wiederum trägt man bei weitergehenden Berechnungen oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
Wenn man sich nur für die zum Ereignis E „Es erscheint die Farbe Gelb genau einmal ‟ gehörigen Ergebnisse interessiert, sähe das Baumdiagramm wie folgt aus:
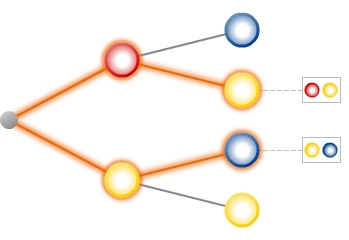
 Beachte hierbei auch die Schreibweise der Ergebnisse als Verkettungen der Anfangsbuchstaben der Farben. Man hätte die Ergebnisse auch als geordnete Paare der Anfangsbuchstaben der Farben angeben können. (R; G) wäre dann das Ergebnis „Linkes Glücksrad bleibt auf Rot stehen - Rechtes Glücksrad bleibt auf Gelb stehen.“
Wiederum trägt man bei weitergehenden Berechnungen oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
Wenn man sich nur für die zum Ereignis E „Es erscheint die Farbe Gelb genau einmal ‟ gehörigen Ergebnisse interessiert, sähe das Baumdiagramm wie folgt aus:
Beachte hierbei auch die Schreibweise der Ergebnisse als Verkettungen der Anfangsbuchstaben der Farben. Man hätte die Ergebnisse auch als geordnete Paare der Anfangsbuchstaben der Farben angeben können. (R; G) wäre dann das Ergebnis „Linkes Glücksrad bleibt auf Rot stehen - Rechtes Glücksrad bleibt auf Gelb stehen.“
Wiederum trägt man bei weitergehenden Berechnungen oft nur die zu einem bestimmten Ereignis gehörigen Ergebnisse ein.
Wenn man sich nur für die zum Ereignis E „Es erscheint die Farbe Gelb genau einmal ‟ gehörigen Ergebnisse interessiert, sähe das Baumdiagramm wie folgt aus:

Welche Zufallsexperimente passen zum angegebenen Baumdiagramm?
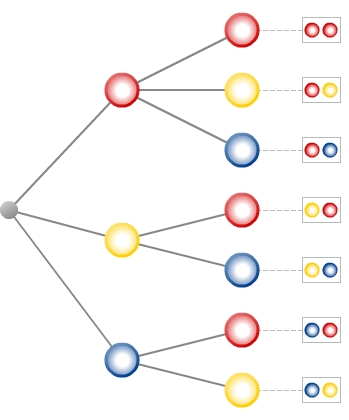


Zufallsexperiment zuordnen
Alle anderen Zufallsexperimente können mindestens eines der beiden Ergebnisse 
 bzw.
bzw. 
 als Ausgang haben. Diese kommen aber im Baumdiagramm nicht vor.
als Ausgang haben. Diese kommen aber im Baumdiagramm nicht vor.

Das abgebildete Glücksrad wird zweimal gedreht. Vervollständige das Baumdiagramm und ordne die zum Ereignis E „Es wird zweimal dieselbe Farbe gedreht ‟ gehörigen Ergebnisse den entsprechenden Endknoten zu.
Vervollständige das Baumdiagramm und ordne die zum Ereignis E „Es wird zweimal dieselbe Farbe gedreht ‟ gehörigen Ergebnisse den entsprechenden Endknoten zu.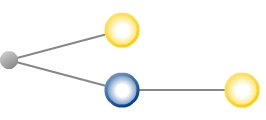
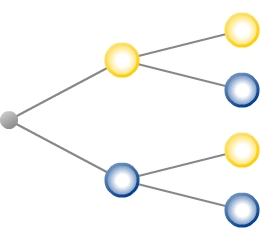
 Vervollständige das Baumdiagramm und ordne die zum Ereignis E „Es wird zweimal dieselbe Farbe gedreht ‟ gehörigen Ergebnisse den entsprechenden Endknoten zu.
Vervollständige das Baumdiagramm und ordne die zum Ereignis E „Es wird zweimal dieselbe Farbe gedreht ‟ gehörigen Ergebnisse den entsprechenden Endknoten zu.
Baumdiagramm ergänzen
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am abgebildeten Glücksrad ‟ entsprechen: und
und  .
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Drehen des abgebildeten Glücksrades“ führen:
.
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Drehen des abgebildeten Glücksrades“ führen: und
und  .
.

Ergebnisse zuordnen
Du ziehst alle diejenigen Ergebnisse an die entsprechenden Positionen im Baumdiagramm, die zu dem Ereignis E - „Es wird zweimal dieselbe Farbe gedreht ‟ - gehören:
 ;
; 
 .
.
Ziehe nun die zum Ereignis E - „Es wird zweimal dieselbe Farbe gedreht“ - gehörigen Ergebnisse an die entsprechenden Endknoten.
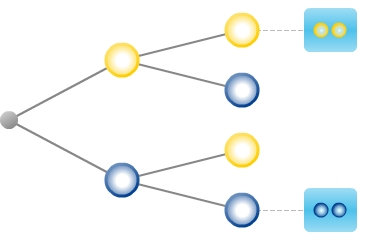

Aus der abgebildeten Urne werden nacheinander zwei Kugeln gezogen, ohne sie zurückzulegen. 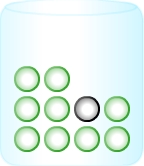 Konstruiere ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend.
Konstruiere ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend.
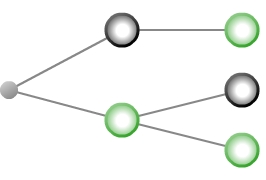
 Konstruiere ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend.
Konstruiere ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend.
Baumdiagramm konstruieren
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Ziehen einer Kugel aus der abgebildeten Urne ‟ entsprechen: und
und  .
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle.
.
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle. In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Ziehen einer Kugel aus der Urne ‟ führen.
Da es nur eine schwarze Kugel gibt und die gezogenen Kugeln nicht zurückgelegt werden, hängen die möglichen Ergebnisse des zweiten Teilexperimentes davon ab, welche Farbe die zuerst gezogene Kugel hat:
Erste Kugel hat Farbe
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Ziehen einer Kugel aus der Urne ‟ führen.
Da es nur eine schwarze Kugel gibt und die gezogenen Kugeln nicht zurückgelegt werden, hängen die möglichen Ergebnisse des zweiten Teilexperimentes davon ab, welche Farbe die zuerst gezogene Kugel hat:
Erste Kugel hat Farbe  :Mögliches Ergebnis des zweiten Teilexperimentes:
:Mögliches Ergebnis des zweiten Teilexperimentes:  Erste Kugel hat Farbe
Erste Kugel hat Farbe  :Mögliche Ergebnisse des zweiten Teilexperimentes:
:Mögliche Ergebnisse des zweiten Teilexperimentes:  und
und 
 In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Ziehen einer Kugel aus der Urne ‟ führen.
Da es nur eine schwarze Kugel gibt und die gezogenen Kugeln nicht zurückgelegt werden, hängen die möglichen Ergebnisse des zweiten Teilexperimentes davon ab, welche Farbe die zuerst gezogene Kugel hat:
Erste Kugel hat Farbe
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Nochmaliges Ziehen einer Kugel aus der Urne ‟ führen.
Da es nur eine schwarze Kugel gibt und die gezogenen Kugeln nicht zurückgelegt werden, hängen die möglichen Ergebnisse des zweiten Teilexperimentes davon ab, welche Farbe die zuerst gezogene Kugel hat:
Erste Kugel hat Farbe 

