Besondere Punkte linearer Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, welche besonderen Punkte eine lineare Funktion hat, wie du sie bestimmst und welche Bedeutung diese Punkte in Sachsituationen haben.
Schnittpunkte der Funktionsgraphen mit den Koordinatenachsen
Jeder Funktionsgraph, der nicht parallel zur x-Achse verläuft, schneidet beide Koordinatenachsen.
Der Schnittpunkt mit der x-Achse hat 0 als y-Koordinate: (
|
)
Der Schnittpunkt mit der y-Achse hat 0 als x-Koordinate: (
|
)
Die Stelle, an der der Graph die x-Achse schneidet, heißt Nullstelle (oder x-Achsenabschnitt), denn das ist der Wert für x, bei dem die Funktion den Wert 0 annimmt: f(
) = 0.
Die Stelle, an der der Graph die y-Achse schneidet, heißt y-Achsenabschnitt:
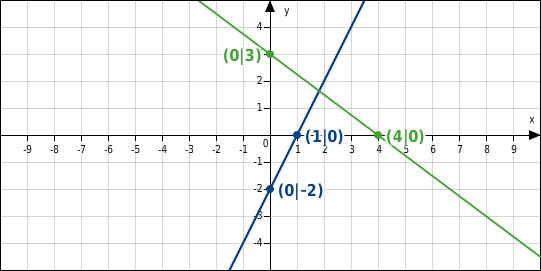
Die Nullstelle der Funktion f ist 4, der y-Achsenabschnitt 3.
Die Nullstelle der Funktion g ist 1, der y-Achsenabschnitt -2.
Berechnen der Nullstelle
Du kannst die Nullstelle
auch mit Hilfe der Funktionsgleichung berechnen.
Der Schnittpunkt mit der x-Achse hat die Koordinaten (
|
).
Du setzt also in der Funktionsgleichung
für y den Wert 0 ein und löst die Gleichung nach x auf.
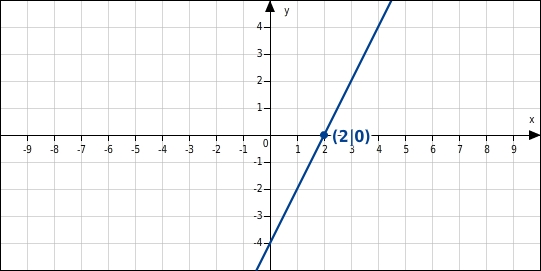
Berechne die Nullstelle der Funktion f mit
.

y-Koordinate einsetzen
Gleichung lösen
Du löst die Gleichung mit Hilfe von äquivalenzumformungen.
Die Nullstelle der Funktion f ist 2.
Der Graph der Funktion schneidet die x-Achse im Punkt (
|
).
 Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
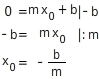
 Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
Allgemein gilt für die Nullstelle
einer Funktion f mit der Funktionsgleichung
und
≠
:
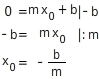

Bestimmen des y-Achsenabschnitts
Den y-Achsenabschnitt einer linearen Funktion kannst du der Funktionsgleichung direkt entnehmen.
In
ist b der y-Achsenabschnitt. Setzt du für x den Wert 0 ein, erhältst du
Der y-Achsenabschnitt dieser Funktion ist 2. Der Graph schneidet die y-Achse im Punkt (
|
).


Der y-Achsenabschnitt dieser Funktion ist -1. Der Graph schneidet die y-Achse im Punkt (
|
).


Berechnen des y-Achsenabschnitts
Wenn vom Graphen einer linearen Funktion ein Punkt und die Steigung gegeben sind, kannst du den y-Achsenabschnitt berechnen.
Bestimme den y-Achsenabschnitt der Funktion f mit der Steigung
, für die der Punkt P(
|
) zum Graphen gehört.

Koordinaten des Punktes in die Funktionsgleichung einsetzen
Du setzt den Wert 1 für y, den Wert 4 für x und den Wert
für m in die Gleichung
ein.

y-Achsenabschnitt bestimmen
Du löst die Gleichung mit Hilfe von äquivalenzumformungen:
 Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
 Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Allgemein gilt für den y-Achsenabschnitt einer Funktion f mit der Funktionsgleichung
und einem gegebenen Punkt P(
|
) auf dem Graphen:
Bedeutung der Achsenabschnitte in Sachsituationen
In Sachsituationen haben die Achsenabschnitte eine besondere Bedeutung.
Der y-Achsenabschnitt steht meist für einen Anfangswert, z. B. Startguthaben, Grundgebühr, Vorsprung usw.
Susanne arbeitet neben ihrem Studium als Aushilfe im Stadttheater an der Garderobe. Sie bekommt vom Veranstalter
Wechselgeld und nimmt dann pro abgegebener Jacke
ein.
Die Zuordnung
Anzahl der Jacken  Betrag in der Kasse in €
kannst du mit einer linearen Funktion beschreiben (
=
):
Der Anfangsbetrag in der Kasse (
) entspricht dem y-Achsenabschnitt.
Betrag in der Kasse in €
kannst du mit einer linearen Funktion beschreiben (
=
):
Der Anfangsbetrag in der Kasse (
) entspricht dem y-Achsenabschnitt.
Die Nullstelle kann z. B. ein Zeitpunkt sein, zu dem ein Becken leer gepumpt ist oder eine Anzahl an Tagen, nach denen ein Vorrat aufgebraucht ist.
Die Nullstelle bildet in Sachsituationen eine Grenze des Definitionsbereichs, wenn die Funktionswerte davor oder danach kleiner als 0 sind und es solche Werte nicht geben kann, z.B. einen negativen Inhalt eines Beckens oder einen negativen Vorrat.
Frau Meier verreist für einige Tage. Damit ihre Pflanzen auf dem Fensterbrett nicht vertrocknen, stellt sie einen Eimer mit
Wasser daneben und verlegt zu jedem Blumentopf einen Wollfaden, der mit einem Ende im Wasser hängt und mit dem anderen Ende in der Erde steckt.
 Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
 Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Das Wasser läuft nun gleichmäßig mit
pro Stunde vom Eimer in die Blumentöpfe.
Die Zuordnung
Anzahl der Stunden  Wassermenge im Eimer in Litern
kannst du mit einer linearen Funktion beschreiben (
=
):
Die Anzahl der Stunden, nach denen der Eimer leer ist, entspricht der Nullstelle der Funktion.
Der Eimer ist nach 45 Stunden leer.
Wassermenge im Eimer in Litern
kannst du mit einer linearen Funktion beschreiben (
=
):
Die Anzahl der Stunden, nach denen der Eimer leer ist, entspricht der Nullstelle der Funktion.
Der Eimer ist nach 45 Stunden leer.
Schnittpunkt zweier Funktionsgraphen
Haben zwei lineare Funktionen verschiedene Steigungen, so schneiden sich die Graphen in einem Punkt.
Dieser Schnittpunkt ist von Bedeutung, wenn du dich z.B. zwischen zwei Möglichkeiten entscheiden möchtest.
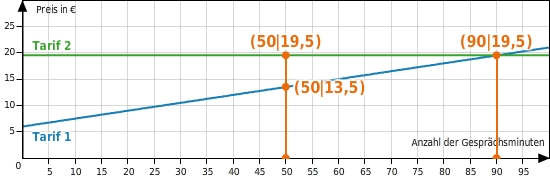
Marie möchte sich ein Handy kaufen und vergleicht vorher einige Handytarife.

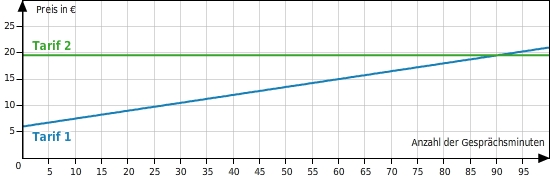 Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?

 Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Welchen Tarif soll Marie wählen, wenn sie voraussichtlich 50 Minuten im Monat telefoniert?
Ab welcher Gesprächsdauer ist die Flatrate günstiger?
Die Geraden mit den Steigungen 0,15 bzw 0 schneiden sich im Punkt (
|
).
Für alle Werte von x, die kleiner sind als 90, verläuft der Graph der Funktion, die den Tarif 1 beschreibt, unterhalb des Graphen der Funktion zu Tarif 2.
Mia sollte also bei einer voraussichtlichen Gesprächsdauer von 50 Minuten pro Monat den Tarif 1 wählen.
Erst ab einer Gesprächsdauer von 90 Minuten wird die Flatrate günstiger.