Besondere Linien im Dreieck
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, welche besonderen Linien (Transversalen) du in Dreiecke einzeichnen kannst, welche Eigenschaften diese Linien haben und wie du diese Linien für weiterführende Betrachtungen zu Dreiecken nutzen kannst.Der Begriff „Transversale“ kommt aus dem Lateinischen und heißt „Durchgehende“ oder „Querende“.Es gibt die Mittelsenkrechten, die Höhen, die Winkelhalbierenden und die Seitenhalbierenden.Wie du die Transversalen konstruieren kannst, lernst du im Thema „Winkel, Grundkonstruktionen und Symmetrie“, denn notwendig ist dazu nur das Konstruieren einer Senkrechten, eines Mittelpunktes oder einer Winkelhalbierenden.
Die Mittelsenkrechten
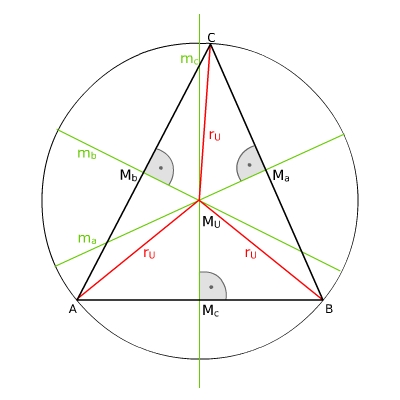
Die Mittelsenkrechten sind Geraden. Sie stehen senkrecht auf den Dreiecksseiten und verlaufen durch deren Mittelpunkte.Die drei Mittelsenkrechten schneiden sich in einem Punkt und dieser Punkt ist der Mittelpunkt des Umkreises des Dreiecks: Denn jeder Punkt einer Mittelsenkrechten hat von den Endpunkten der zugehörigen Dreiecksseite jeweils den gleichen Abstand, also hat der Schnittpunkt der Mittelsenkrechten von allen drei Eckpunkten den gleichen Abstand.Insbesondere gibt es zu jedem Dreieck genau einen Kreis, der durch die drei Eckpunkte verläuft, den Umkreis des Dreiecks.Der Radius des Umkreises entspricht also den Strecken
.

Konstruiere den Umkreis des Dreiecks ABC.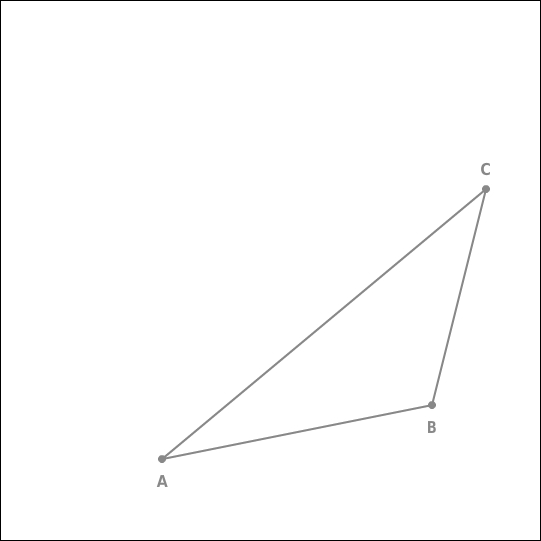



Mittelsenkrechte konstruieren
Zur Konstruktion der Mittelsenkrechten verwendest du den Zirkel. Du zeichnest um die Punkte A und B jeweils einen Kreis mit gleichem Radius. Dabei wählst du den Radius so, dass sich die Kreise in zwei Punkten schneiden. Die Gerade, die diese beiden Schnittpunkte verbindet, ist die Mittelsenkrechte der Seite c.
Die anderen beiden Mittelsenkrechten wurden in diesem Beispiel mit den Werkzeugen „Mittelpunkt“ und „Senkrechte“ gezeichnet. Konstruierst du selbst auf dem Papier, dann solltest du immer den Zirkel benutzen, da du mit dem Geodreieck den Mittelpunkt einer Seite nicht genau bestimmen kannst.

Umkreis zeichnen
Um den Mittelpunkt
des Umkreises zu finden, hätten auch zwei Mittelsenkrechte genügt. Die dritte Mittelsenkrechte kannst du zur Kontrolle konstruieren. Wenn sie die beiden ersten Geraden nicht in deren Schnittpunkt schneidet, dann hast du unsauber gezeichnet.
Der Schnittpunkt der Mittelsenkrechten liegt bei einem stumpfwinkligen Dreieck außerhalb des Dreiecks.
Den Umkreis zeichnest du, indem du
als Mittelpunkt wählst und den Radius
oder
oder
in den Zirkel nimmst. Auch jetzt kannst du wieder kontrollieren, ob du sauber gezeichnet hast, denn alle drei Punkte des Dreiecks müssen auf dem Umkreis liegen.

Konstruiere den Mittelpunkt des Kreises.
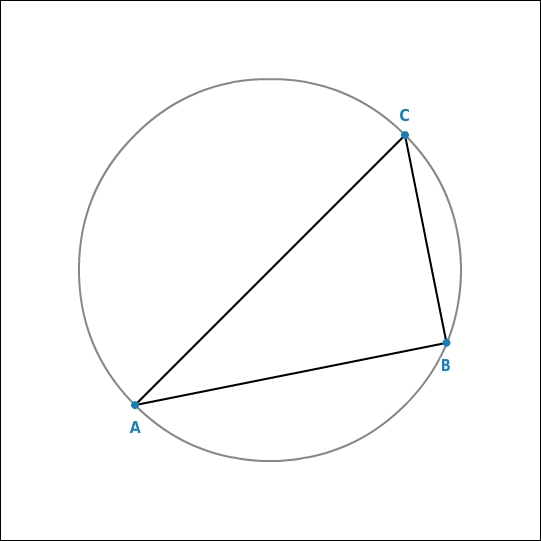
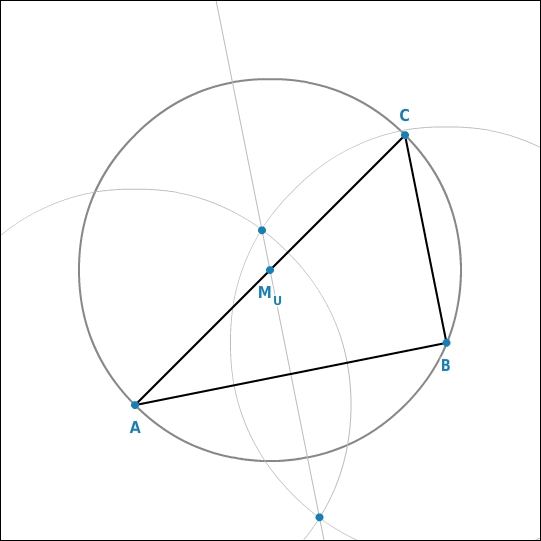

Lösungsidee finden
Du zeichnest also ein Dreieck, dessen Eckpunkte auf der Kreislinie liegen. Der Kreis ist dann der Umkreis des Dreiecks. Du konstruierst also zu mindestens zwei Seiten des Dreiecks die Mittelsenkrechten und erhältst so den Mittelpunkt des Umkreises als Schnittpunkt.
Der Mittelpunkt eines Kreises ist immer der Schnittpunkt der Mittelsenkrechten jedes Dreiecks, dessen Eckpunkte auf der Kreislinie liegen.
Dreieck zeichnen
Bei einem rechtwinkligen Dreieck ist die Seite, die dem rechten Winkel gegenüber liegt, immer ein Durchmesser des Umkreises. Der Mittelpunkt des Umkreises ist also der Mittelpunkt der dem rechten Winkel gegenüberliegenden Seite.

Mittelpunkt konstruieren
Den Mittelpunkt konstruierst du mit dem Zirkel. überprüfe deine Konstruktion, indem du einen Kreis mit dem Mittelpunkt
und dem Radius
zeichnest. Der Kreis stimmt mit dem gegebenen Kreis überein.

Die Winkelhalbierenden
Die Winkelhalbierenden sind Halbgeraden. Sie beginnen im Eckpunkt und halbieren jeweils den Winkel, der an dem Eckpunkt anliegt.Die drei Winkelhalbierenden schneiden sich in einem Punkt innerhalb des Dreiecks. Dieser Punkt ist der Mittelpunkt des Inkreises des Dreiecks: Denn jeder Punkt einer Winkelhalbierenden hat von den Seiten, die die Schenkel des Winkels sind, jeweils den gleichen Abstand. Also hat der Schnittpunkt der Winkelhalbierenden von allen drei Seiten des Dreiecks den gleichen Abstand.Der Inkreis berührt die drei Seiten jeweils in einem Punkt. Die Dreiecksseiten sind also Tangenten des Inkreises. Der Radius des Inkreises steht an den Berührungspunkten senkrecht auf den Dreiecksseiten.Insbesondere gibt es zu jedem Dreieck genau einen Kreis, der innerhalb des Dreiecks liegt und alle drei Seiten berührt: Den Inkreis des Dreiecks.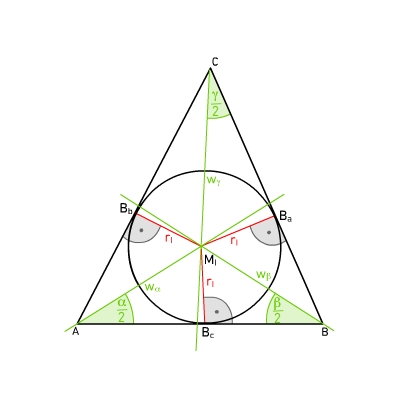

Konstruiere den Inkreis des Dreiecks ABC.
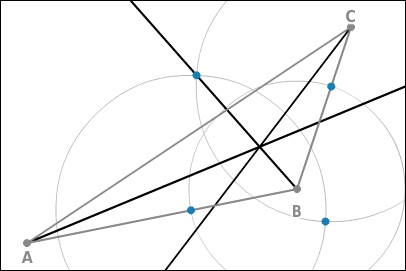


Winkelhalbierende konstruieren
Zur Konstruktion der Winkelhalbierenden verwendest du den Zirkel. Du zeichnest z. B. um den Punkt B einen Kreis Dieser Kreis schneidet die Seiten c und a. Um diese Schnittpunkte zeichnest du wieder jeweils einen Kreis mit einem Radius so, dass sich die beiden Kreise zweimal schneiden. Die Gerade, die den Punkt B und den Schnittpunkt der Kreise, der dem Winkel gegenüberliegt, verbindet, ist die Winkelhalbierende des Winkels
.Die anderen beiden Winkelhalbierenden wurden genauso konstruiert. Für die übersichtlichkeit wurden aber die Kreise wieder gelöscht.

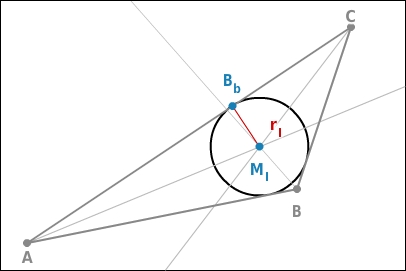
Inkreisradius konstruieren
Um den Mittelpunkt
des Inkreises zu finden, hätten auch zwei Winkelhalbierende genügt. Die dritte Winkelhalbierende kannst du zur Kontrolle konstruieren. Wenn sie die beiden ersten Geraden nicht in deren Schnittpunkt schneidet, dann hast du unsauber gezeichnet.Um den Radius des Inkreises zu finden, konstruierst du vom Mittelpunkt M ein Lot auf eine der Dreiecksseiten. Der Schnittpunkt des Lotes mit der Dreiecksseite ist der Berührungspunkt des Inkreises mit dieser Dreiecksseite. Also ist die Strecke
der Radius des Inkreises.

Inkreis zeichnen
Den Inkreis zeichnest du nun mit dem Zirkel. Wenn du sauber konstruiert hast, dann berührt der Inkreis die beiden anderen Dreiecksseiten auch jeweils in genau einem Punkt.

Jedes Dreieck hat auch drei Ankreise, die jeweils eine Seite und die Verlängerungen der anderen beiden Seiten in jeweils einem Punkt berühren.Den Mittelpunkt des Ankreises der Seite c findest du, indem du die Winkelhalbierenden des Winkels
und die der Außenwinkel in den Punkten A und B konstruierst. Diese schneiden sich im Mittelpunkt des Ankreises.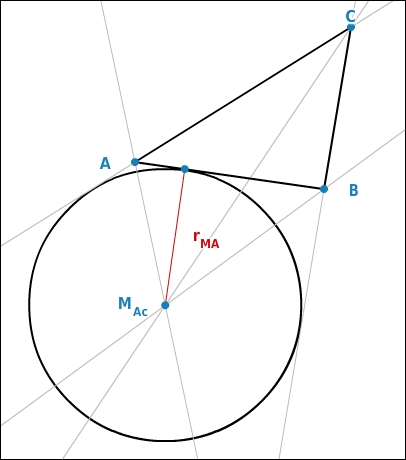

Um den Radius zu finden, musst du wieder vom Mittelpunkt aus das Lot auf die Seite c fällen.
Die Höhen
Die Höhen sind Strecken. Sie stehen senkrecht auf den Dreiecksseiten und enden im jeweils gegenüberliegenden Eckpunkt. Die drei Höhen oder deren Verlängerungen schneiden sich in einem Punkt. Die drei Höhenfußpunkte in einem spitzwinkligen Dreieck kannst du zum Höhenfußpunktdreieck verbinden. In diesem Höhenfußpunktdreieck sind die Höhen des ursprünglichen Dreiecks dann die Winkelhalbierenden.Der Schnittpunkt der Höhen ist in einem spitzwinkligen Dreieck also der Mittelpunkt des Inkreises des Höhenfußpunktdreiecks.

Konstruiere die Höhen im stumpfwinkligen Dreieck ABC.
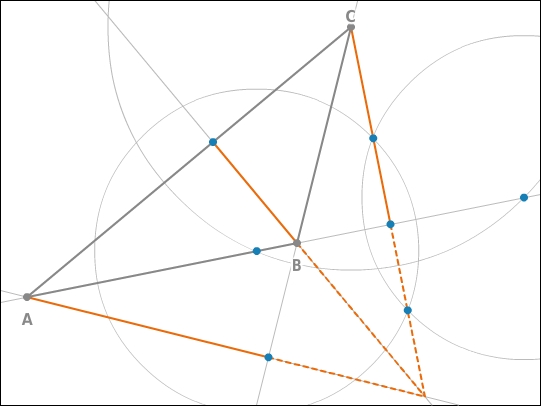

Höhen konstruieren
Zur Konstruktion einer Höhe verwendest du den Zirkel. Du fällst das Lot vom Punkt C auf die Verlängerung der Seite c. Die anderen beiden Höhen wurden in diesem Beispiel mit dem Werkzeug „Senkrechte“ gezeichnet. Die Höhen der Seiten, die die Schenkel des stumpfen Winkels sind, liegen außerhalb des Dreiecks.Auch der Schnittpunkt der Höhenverlängerungen liegt außerhalb.

Konstruiere das Höhenfußpunktdreieck des rechtwinkligen Dreiecks ABC.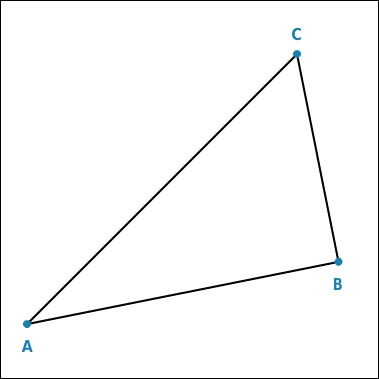
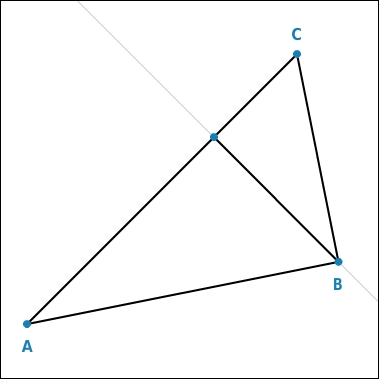

Höhen konstruieren
In einem rechtwinkligen Dreieck musst du nur eine Höhe konstruieren, nämlich die auf der Seite, die dem rechten Winkel gegenüberliegt. Die anderen beiden Höhen sind schon da, es sind die Dreiecksseiten, die den rechten Winkel bilden. Die Höhen schneiden sich also alle in dem Punkt, an dem der rechte Winkel anliegt, in diesem Beispiel im Punkt B.

Höhenfußpunktdreieck zeichnen
Ein Höhenfußpunktdreieck existiert nicht, da bei der Höhenkonstruktion nur zwei verschiedene Höhenfußpunkte entstanden sind.
Die Seitenhalbierenden
Die Seitenhalbierenden sind die Verbindungsstrecken zwischen den Eckpunkten und dem Seitenmittelpunkt der gegenüberliegenden Seite. Die drei Seitenhalbierenden schneiden sich immer in einem Punkt innerhalb des Dreiecks, dem Schwerpunkt des Dreiecks. Deshalb werden die Seitenhalbierenden auch Schwerelinien genannt.Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2:1, die Strecke
ist also doppelt so lang wie die Strecke
. Würdest du ein dreieckiges Brett am Schwerpunkt aufhängen, so würde es waagerecht zum Boden „schweben“. Die Seiten des Seitenmittendreiecks
sind parallel zu den Dreiecksseiten des Dreiecks .Die Dreiecke
,
,
und
sind kongruent.Die Seitenhalbierenden des Dreiecks schneiden die Seiten des Seitenmittendreiecks auch in ihren Mittelpunkten, die Seitenhalbierenden des Dreiecks sind also auch die Seitenhalbierenden des Dreiecks
. Deshalb sind die Schwerpunkte der Dreiecke und
identisch.
Die Seiten des Seitenmittendreiecks
sind parallel zu den Dreiecksseiten des Dreiecks .Die Dreiecke
,
,
und
sind kongruent.Die Seitenhalbierenden des Dreiecks schneiden die Seiten des Seitenmittendreiecks auch in ihren Mittelpunkten, die Seitenhalbierenden des Dreiecks sind also auch die Seitenhalbierenden des Dreiecks
. Deshalb sind die Schwerpunkte der Dreiecke und
identisch.
 Die Seiten des Seitenmittendreiecks
sind parallel zu den Dreiecksseiten des Dreiecks .Die Dreiecke
,
,
und
sind kongruent.Die Seitenhalbierenden des Dreiecks schneiden die Seiten des Seitenmittendreiecks auch in ihren Mittelpunkten, die Seitenhalbierenden des Dreiecks sind also auch die Seitenhalbierenden des Dreiecks
. Deshalb sind die Schwerpunkte der Dreiecke und
identisch.
Die Seiten des Seitenmittendreiecks
sind parallel zu den Dreiecksseiten des Dreiecks .Die Dreiecke
,
,
und
sind kongruent.Die Seitenhalbierenden des Dreiecks schneiden die Seiten des Seitenmittendreiecks auch in ihren Mittelpunkten, die Seitenhalbierenden des Dreiecks sind also auch die Seitenhalbierenden des Dreiecks
. Deshalb sind die Schwerpunkte der Dreiecke und
identisch.

