Teilbarkeitsregeln anwenden
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du die Teilbarkeitsregeln anwenden kannst.
Teilbarkeit durch spezielle Produkte
Für einige Zahlen kannst du die Teilbarkeit durch diese anhand ihrer Faktoren überprüfen.
Wenn eine Zahl durch 3 und 4 teilbar ist, so ist sie auch durch deren Produkt
teilbar.
Wenn eine Zahl durch 3 und 5 teilbar ist, so ist sie auch durch deren Produkt
teilbar.
Wenn eine Zahl durch 2 und 9 teilbar ist, so ist sie auch durch deren Produkt
teilbar.
Teilbarkeitsregel zur 12: Eine Zahl ist durch 12 teilbar, wenn sie durch 3 und durch 4 teilbar ist, sonst nicht.
Teilbarkeitsregel zur 15: Eine Zahl ist durch 15 teilbar, wenn ihre Quersumme, das heißt die Summe ihrer Ziffern, durch 3 teilbar ist und ihre letzte Ziffer 0 oder 5 ist, sonst nicht.
Teilbarkeitsregel zur 18: Eine Zahl ist durch 18 teilbar, wenn sie gerade ist und ihre Quersumme, das heißt die Summe ihrer Ziffern, durch 9 teilbar ist, sonst nicht.
Teilbarkeit durch 12
648 ist durch 12 teilbar.
Teilbarkeit durch 3:Die Quersumme von 648 ist 18. Wie du siehst, fällt bei der Division kein Rest an
, also ist 18 durch 3 teilbar.
Teilbarkeit durch 4:
hat die Endziffern 48. Da
keinen Rest ergibt, ist 48 durch 4 teilbar.
648 ist durch 3 und 4 teilbar, also ist 648 auch durch 12 teilbar.
646 ist nicht durch 12 teilbar.
Teilbarkeit durch 3:Die Quersumme von 646 ist 16. Da
R 1 einen Rest ergibt, ist 16 nicht durch 3 teilbar.
Die Teilbarkeit durch 4 muss damit nicht mehr überprüft werden.
646 ist nicht durch 3 teilbar, also ist sie auch nicht durch 12 teilbar.
Wenn die Zahl ungerade ist, kann sie nicht durch 12 teilbar sein.
645 ist nicht durch 12 teilbar.
645 ist eine ungerade Zahl, kann also nicht durch 4 teilbar sein.
645 ist nicht durch 4 teilbar, also ist sie auch nicht durch 12 teilbar.
Teilbarkeit durch 15
135 ist durch 15 teilbar.
Teilbarkeit durch 3:Die Quersumme von 135 ist 9. Da
keinen Rest ergibt, ist 9 durch 3 teilbar.
Teilbarkeit durch 5:
hat die Endziffer 5 und ist damit durch 5 teilbar.
135 ist durch 3 und 5 teilbar, also ist sie auch durch 15 teilbar.
235 ist nicht durch 15 teilbar.
Teilbarkeit durch 3:Die Quersumme von 235 ist 10. Da
R 1 einen Rest ergibt, ist 10 nicht durch 3 teilbar.
Die Teilbarkeit durch 5 muss damit nicht mehr überprüft werden.
235 ist nicht durch 3 teilbar, also ist sie auch nicht durch 15 teilbar.
Teilbarkeit durch 18
288 ist durch 18 teilbar.
Teilbarkeit durch 2:
hat die Endziffer 8 und ist damit durch 2 teilbar.
Teilbarkeit durch 9:Die Quersumme von 288 ist 18. Da
keinen Rest ergibt, ist 18 durch 9 teilbar.Wenn die Quersumme einer Zahl durch 9 teilbar ist, so ist auch die Zahl selbst durch 9 teilbar.
288 ist durch 2 und 9 teilbar, also ist sie auch durch 18 teilbar.
729 ist nicht durch 18 teilbar.
Teilbarkeit durch 2:
hat die Endziffer 9 und ist damit nicht durch 2 teilbar.
Die Teilbarkeit durch 9 muss damit nicht mehr überprüft werden
729 ist nicht durch 2 teilbar, also ist sie auch nicht durch 18 teilbar
Teilbarkeit von Produkten
Manchmal kennst du bei einem Produkt schon einen der Faktoren (zum Beispiel bei dir bekannten Quadratzahlen).
Ist dieser Faktor durch eine Zahl teilbar, so ist auch das Produkt durch diese Zahl teilbar.
Teilbarkeitsregel für Produkte: Teilt eine Zahl einen der Faktoren eines Produkts, so teilt sie auch das Produkt.
144 ist durch 3 teilbar.
Du weißt, dass 144 eine Quadratzahl ist:
12 ist durch 3 teilbar, also muss auch 144 durch 3 teilbar sein.
Die Umkehrung gilt jedoch nicht:Ist das Produkt durch eine Zahl teilbar, muss noch lange nicht auch jeder Faktor durch diese Zahl teilbar sein.
24 ist durch 8 teilbar.
, aber weder 6 noch 4 sind durch 8 teilbar.
Teilbarkeit von Summen und Differenzen
Wenn du die Teilbarkeitsregeln nicht direkt auf eine Zahl anwenden kannst, ist es hilfreich die Zahl als Summe oder Differenz zu schreiben.
Teilbarkeit einer Summe:Wenn jeder Summand durch eine gegebene Zahl teilbar ist, so ist auch die Summe durch diese Zahl teilbar.Ist nur einer der Summanden durch eine Zahl teilbar und der andere nicht, so ist auch die Summe nicht durch diese Zahl teilbar.
Teilbarkeit einer Differenz:Sind der Minuend und der Subtrahend einer Differenz durch eine gegebene Zahl teilbar, so ist auch die Differenz durch diese Zahl teilbar.Ist entweder der Minuend oder der Subrahend der beiden nicht durch eine gegebene Zahl teilbar, so auch nicht die Differenz.
Teilbarkeitsregel einer Summe: Teilt eine Zahl jeden Summanden einer Summe, so teilt sie auch die Summe.
Teilbarkeitsregel einer Differenz: Teilt eine Zahl den Minuenden und den Subtrahenden einer Differenz, so teilt sie auch die Differenz.
6391 ist durch 7 teilbar.
Zerlege 6391 in eine Summe. Die Summanden solltest du im Kopf durch 7 dividieren können:
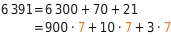 Sowohl 6300 als auch 70 und 21 sind durch
teilbar.
Sowohl 6300 als auch 70 und 21 sind durch
teilbar.
729 ist nicht durch 7 teilbar.
Zerlege 729 in eine Summe. Die Summanden solltest du im Kopf durch 7 dividieren können:
 Sowohl 700 als auch 28 sind durch 7 teilbar. Es bleibt jedoch der Rest 1.
Sowohl 700 als auch 28 sind durch 7 teilbar. Es bleibt jedoch der Rest 1.
728 ist durch 8 teilbar.
Zerlege 728 in eine Summe. Die Summanden solltest du im Kopf durch 8 dividieren können:
 Sowohl 720 als auch 8 sind durch
teilbar, also ist auch 728 durch 8 teilbar.
Sowohl 720 als auch 8 sind durch
teilbar, also ist auch 728 durch 8 teilbar.
Teilbarkeit einer Differenz
98 ist nicht durch 4 teilbar.
Zerlege 98 in eine Differenz. Den Minuenden und den Subtrahenden solltest du im Kopf durch 4 dividieren können:
 100 ist durch
teilbar, jedoch ist 2 nicht durch 4 teilbar, also ist 98 nicht durch 4 teilbar.
100 ist durch
teilbar, jedoch ist 2 nicht durch 4 teilbar, also ist 98 nicht durch 4 teilbar.

