Rechnen mit Potenzen und Wurzeln
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenZehnerpotenzen
mit der
10 heißen
. Der
gibt die Anzahl der Nullen an, die du benötigst, um die Potenz als natürliche Zahl bzw. als
zu schreiben.
.
.

Wissenschaftliche Schreibweise
Um sehr große und sehr kleine positive Zahlen übersichtlich aufschreiben zu können, trennst du
ab.
Bei jeder endlichen Dezimalzahl kannst du das Komma so verschieben, dass nur eine Ziffer vor dem Komma steht, indem du mit einer Zehnerpotenz multiplizierst. Die Zehnerpotenz schreibst du als
dahinter. Der
der Zehnerpotenz ist gleich der
, um die du das Komma nach links (positiver Exponent) oder rechts (negativer Exponent) verschoben hast.
Diese Darstellung heißt wissenschaftliche Schreibweise.
Du zählst die Stellen, um die du das Komma nach
verschiebst bis die Dezimalzahl genau eine, von Null verschiedene Ziffer vor dem Komma hat.
Du zählst die Stellen, um die du das Komma nach
verschiebst bis die Dezimalzahl genau eine, von Null verschiedene Ziffer vor dem Komma hat.
Zahlen in wissenschaftlicher Schreibweise kann man leicht vergleichen. Dazu vergleichst du entweder nur die Exponenten der abgetrennten Zehnerpotenz oder, falls diese gleich sind, nur die Dezimalzahlen davor.
, da
.
Die Exponenten sind gleich, aber
.
Potenzen mit rationalen Exponenten
Für eine positive reelle Zahl a und natürliche Zahlen
,
wird vereinbart:
und
Für positive Exponenten darf auch
sein:
Du kannst jede
mit rationalem
und jede Potenz mit rationalem Exponenten als Wurzel schreiben.
Insbesondere lassen sich damit
als Potenzen mit rationalen Exponenten schreiben.
Die n-te Potenz

Für eine reelle Zahl a und eine natürliche Zahl
ist:
Sprich: a hoch n

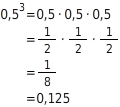
Potenzen mit negativer Basis
Das Produkt aus einer geraden Anzahl negativer Faktoren ist positiv. Damit ist auch eine Potenz mit negativer Basis und geradem Exponenten positiv.

Das Produkt aus einer
Anzahl negativer Faktoren ist negativ. Damit ist auch eine Potenz mit negativer Basis und
Exponenten negativ.

Steht vor der Potenz ein negatives Vorzeichen, bildest du die Gegenzahl.Du berechnest also die Potenz zunächst ohne das Vorzeichen zu beachten und änderst anschließend das Vorzeichen.


Potenzgesetze
1. Für eine ganze Zahl n und eine reelle Zahl
≠
ist
.2. Für eine reelle Zahl
≠
ist
3. Für eine ganze Zahl n und reelle Zahlen a und b, beide ungleich 0, ist
.
Die
für
mit natürlichen
gelten auch für Potenzen mit ganzzahligen Exponenten.
4. Für ganze Zahlen m und n und eine reelle Zahl
≠
gilt:
und
5. Für eine ganze Zahl n und reelle Zahlen a,b≠
gilt:
und
6. Für ganze Zahlen m und n und eine reelle Zahl
≠
gilt:

