Rationale Zahlen im Koordinatensystem
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du mit einem Koordinatensystem umgehst, in dem auch negative Zahlen vorkommen.
Das vollständige Koordinatensystem
Der Zahlenstrahl wird zu einer Zahlengerade erweitert, indem du negative Zahlen mit aufnimmst. Ebenso kann man auch das Koordinatensystem erweitern. Zahlenstrahl
Zahlengerade
Du kannst das dir bekannte Quadratgitter auf den negativen Bereich ausdehnen, indem du die x- und die y-Achse über den Nullpunkt hinweg zu Zahlengeraden ausdehnst. Denn ein Koordinatensystem ist nichts anderes als zwei Zahlengeraden, die senkrecht aufeinander stehen. QuadratgitterKoordinatensystem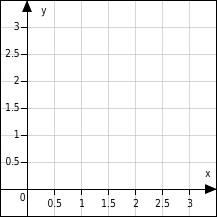 
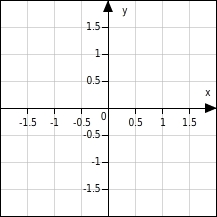Diese beiden Zahlengeraden werden auch Koordinatenachsen genannt. In der Mathematik nennt man die x-Achse auch die Abzisse und die y-Achse die Ordinate. Der Punkt O (0|0), in dem sich die beiden Achsen schneiden, wird auch als Ursprung bezeichnet.
Die Quadranten des Koordinatensystems
Die beiden Koordinatenachsen unterteilen die Zeichenebene in vier Quadranten (also in vier Felder).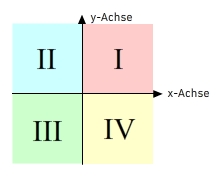
Auch wenn du einen Punkt nicht zeichnest, kannst du an den Vorzeichen seiner Koordinaten erkennen in welchem Quadranten der Punkt liegt. P(x/y) 
Ein Punkt im Koordinatensystem
Ein Punkt im Koordinatensystem wird durch seine x-Koordinate (auch x-Wert genannt) und seine y-Koordinate (auch y-Wert genannt) beschrieben.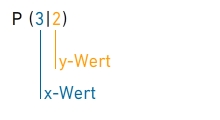
Alle Punkte werden mit Großbuchstaben benannt (A, P, R, T, ...).
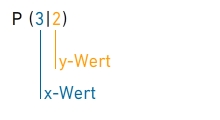
Einzeichnen eines Punkts
Wenn du einen Punkt in das Koordinatensystem einzeichnen möchtest, dann trägst du die x- und y-Werte immer vom Ursprung aus parallel zu den Achsen ab: x-Wert positiv: waagerecht nach rechts abtragenx-Wert negativ:waagerecht nach links abtragen y-Wert positiv: senkrecht nach oben abtrageny-Wert negativ: senkrecht nach unten abtragen
A(3|2)
A(-4|3)
A(-2|-3)
A(4|-1)
Ablesen eines Punkts
Wenn du einen Punkt ablesen möchtest, dann denke dir durch den Punkt zwei Geraden, die zu den Koordinatenachsen parallel verlaufen. Dort, wo die Geraden die Koordinatenachsen schneiden, kannst du den x- und den y-Wert des Punkts ablesen.
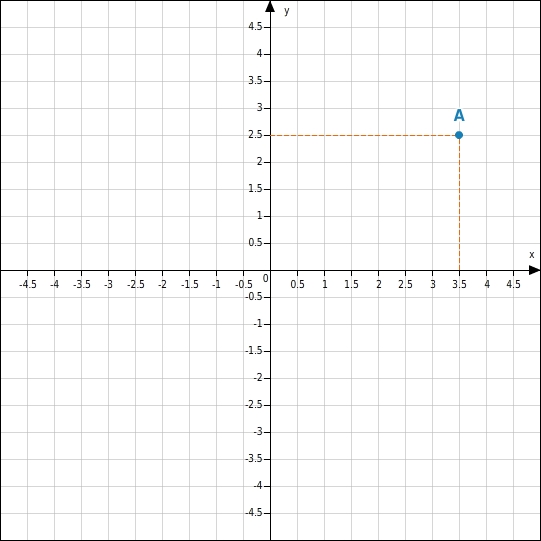
Geraden im Koordinatensystem
Um eine Gerade in das Koordinatensystem einzuzeichnen, verbindest du zwei Punkte miteinander, durch die diese Gerade verlaufen soll. Geraden werden mit Kleinbuchstaben bezeichnet (g, h, j, k, ...).
Gerade g durch die Punkte A(2|1) und B(-4|-3)
Spiegeln von Punkten im Koordinatensystem
Bei einer Spiegelung eines Punktes an einer Koordinatenachse oder am Ursprung ist der Abstand des Punktes von der Spiegelachse oder dem Ursprung immer genauso groß, wie der Abstand des Spiegelpunktes von der Spiegelachse oder dem Ursprung.
Spiegelung an der x-Achse:
Wenn du einen Punkt an der x-Achse spiegelst, dann verändert sich nur das Vorzeichen der y-Koordinate des Punktes.
Spiegelung an der y-Achse:
Wenn du einen Punkt an der y-Achse spiegelst, dann verändert sich nur das Vorzeichen des x-Koordinate des Punktes.
Spiegelung am Ursprung:
Wenn du einen Punkt am Ursprung spiegelst, kehren sich die Vorzeichen beider Koordinaten des Punktes um.
