Kreisausschnitt und Kreisbogen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du den Flächeninhalt von Kreisausschnitten und Kreisabschnitten und die Länge von Kreisbögen berechnen kannst.
Kreisausschnitt
Wählst du auf einer Kreislinie zwei Punkte aus und verbindest diese mit dem Kreismittelpunkt, dann erhältst du einen Ausschnitt des Kreises. Der Flächeninhalt des Kreisausschnitts
(auch Kreissektor genannt) wird bestimmt durch die Größe des Mittelpunktswinkels
. Je größer der Winkel
ist, desto größer ist auch der Flächeninhalt des Kreisausschnitts.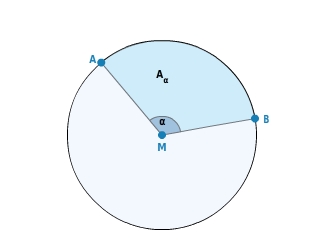 Den Flächeninhalt eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht der Kreisausschnitt einem Drittel des Vollkreises, denn 120 ist der dritte Teil von 360.
=
Allgemein gilt für den Flächeninhalt eines Kreisausschnitts mit dem Winkel
:
Den Flächeninhalt eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht der Kreisausschnitt einem Drittel des Vollkreises, denn 120 ist der dritte Teil von 360.
=
Allgemein gilt für den Flächeninhalt eines Kreisausschnitts mit dem Winkel
:
 Den Flächeninhalt eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht der Kreisausschnitt einem Drittel des Vollkreises, denn 120 ist der dritte Teil von 360.
=
Allgemein gilt für den Flächeninhalt eines Kreisausschnitts mit dem Winkel
:
Den Flächeninhalt eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht der Kreisausschnitt einem Drittel des Vollkreises, denn 120 ist der dritte Teil von 360.
=
Allgemein gilt für den Flächeninhalt eines Kreisausschnitts mit dem Winkel
:
Für den
mit dem Radius r und dem Mittelpunktswinkel
gilt:
Für einen
ergibt sich:
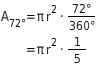
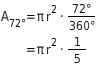
Gegeben sind der Radius r =
und der Mittelpunktswinkel
eines Kreises. Berechne den Flächeninhalt des Kreisausschnitts.Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Kreisausschnittfläche berechnen
Du setzt den Radius r =
und den Mittelpunktswinkel
in die Formel für den Flächeninhalt des Kreisausschnitts ein:
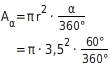 Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Berechne alle Teilergebnisse, bei denen du nicht runden musst:
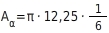
 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 6,41
So vermeidest du Fehler durch zu häufiges Runden der Zwischenergebnisse.
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 6,41
So vermeidest du Fehler durch zu häufiges Runden der Zwischenergebnisse.
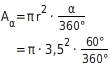 Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Der Kreisausschnitt hat einen Flächeninhalt von etwa 6,41
.
Kreisbogen
Der zu einem Kreisausschnitt gehörende Teil der Kreislinie wird als Kreisbogen bezeichnet. Die Länge des Kreisbogens b ist abhängig von der Größe des Mittelpunktswinkels
. Je größer der Winkel
, desto länger ist der Kreisbogen.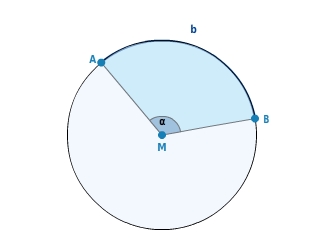 Den Umfang eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht die Kreisbogenlänge einem Drittel des Vollkreisumfangs, denn 120 ist derdritte Teil von 360.
Allgemein gilt für die Bogenlänge:
Den Umfang eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht die Kreisbogenlänge einem Drittel des Vollkreisumfangs, denn 120 ist derdritte Teil von 360.
Allgemein gilt für die Bogenlänge:
 Den Umfang eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht die Kreisbogenlänge einem Drittel des Vollkreisumfangs, denn 120 ist derdritte Teil von 360.
Allgemein gilt für die Bogenlänge:
Den Umfang eines vollen Kreises (
) berechnest du mit der Formel
. Ist zum Beispiel
, dann entspricht die Kreisbogenlänge einem Drittel des Vollkreisumfangs, denn 120 ist derdritte Teil von 360.
Allgemein gilt für die Bogenlänge:
Für die
mit dem Mittelpunktswinkel
und dem Radius r gilt:
Für einen
ergibt sich:
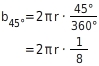
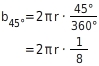
Gegeben sind der Radius r =
und der Mittelpunktswinkel
eines Kreises. Berechne die Länge des Kreisbogens.Gib das Ergebnis auf eine Stelle nach dem Komma genau an.
Kreisbogenlänge berechnen
Du setzt den Radius r =
und den Mittelpunktswinkel
in die Formel für den Kreisbogens ein:
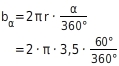 Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Berechne alle Teilergebnisse, bei denen du nicht runden musst:

 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 3,7
So vermeidest du Fehler durch zu häufiges Runden der Zwischenergebnisse.
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
≈ 3,7
So vermeidest du Fehler durch zu häufiges Runden der Zwischenergebnisse.
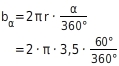 Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Berechne alle Teilergebnisse, bei denen du nicht runden musst:
Der Kreisbogen hat eine Länge von etwa
.
Kreisabschnitt
Der Kreisabschnitt (auch Kreissegment genannt)
ist Teil eines Kreisausschnitts. Der Kreisabschnitt wird von der Sehne s und dem zugehörigen Kreisbogen b begrenzt.

Den
berechnest du, indem du vom Flächeninhalt des Kreisausschnitts (
) den Flächeninhalt des Dreiecks MAB (
) subtrahierst:
=
-
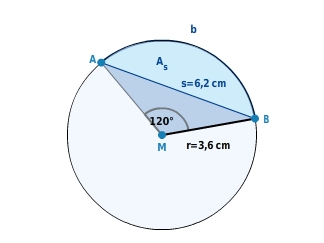
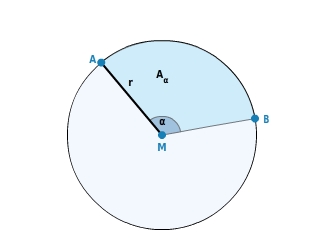 Du setzt den Radius r =
und den Mittelpunktswinkel
in die Formel für den Flächeninhalt des Kreisausschnitts ein:
Du setzt den Radius r =
und den Mittelpunktswinkel
in die Formel für den Flächeninhalt des Kreisausschnitts ein:
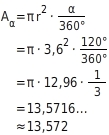
 =
s
h
Das Dreieck MAB ist gleichschenklig, denn zwei Seiten sind gleichzeitig Radius im Kreis.Die Höhe h halbiert also die Sehne s und teilt das Dreieck MAB in zwei rechtwinklige Dreiecke mit der Hypotenuse r.Du kannst die Höhe h mit dem Satz des Pythagoras bestimmen:
=
+
=
-
h =
Also:
=
s
Du setzt den Radius r =
und die Sehne s =
in die Formel ein:
=
s
h
Das Dreieck MAB ist gleichschenklig, denn zwei Seiten sind gleichzeitig Radius im Kreis.Die Höhe h halbiert also die Sehne s und teilt das Dreieck MAB in zwei rechtwinklige Dreiecke mit der Hypotenuse r.Du kannst die Höhe h mit dem Satz des Pythagoras bestimmen:
=
+
=
-
h =
Also:
=
s
Du setzt den Radius r =
und die Sehne s =
in die Formel ein:
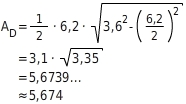 Vom Flächeninhalt des Kreisausschnitts
subtrahierst du den Flächeninhalt des Dreiecks MAB
.
Vom Flächeninhalt des Kreisausschnitts
subtrahierst du den Flächeninhalt des Dreiecks MAB
.
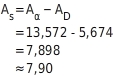
Da die Werte für die Sehne und den Radius nur auf eine Stelle nach dem Komma genau angegeben sind, ist es sinnvoll, das Ergebnis auf höchstens zwei Stellen nach dem Komma zu runden.

