Grundlagen zu den Strahlensätzen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du etwas über den ersten und zweiten Strahlensatz, wie du die beiden Strahlensätze anhand von Strahlensatzfiguren wiedergibst und voneinander unterscheidest.
Strahlensatz und die Anwendung
Die Strahlensätze werden sowohl in der Geometrie als auch in der praktischen Anwendung genutzt. Sie ergeben sich aus den Eigenschaften der zentrischen Streckung. Bei der zentrischen Streckung werden alle Strecken einer Zeichnung im gleichen Verhältnis vergrößert oder verkleinert. Die Bildstrecken stehen im selben Verhältnis zueinander wie die Originalstrecken.
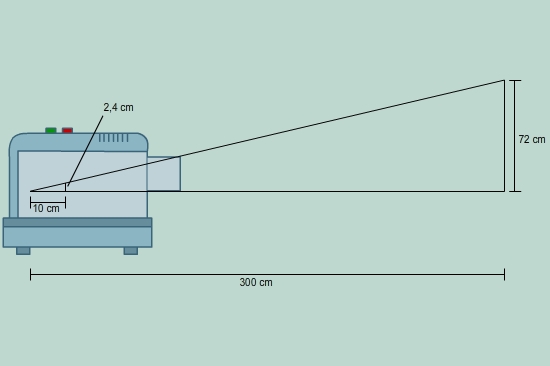

Bei einer Familienfeier möchte Opa Schulz seiner großen Familie alte Dias zeigen.
Er stellt den Diaprojektor in einer Entfernung von
(
) zur Wand auf. Die Dias sind
hoch und
breit. Die Glühlampe im Projektor ist
vom Dia entfernt. Das Bild an der Wand ist
hoch.
Die Familienmitglieder in der letzten Reihe können allerdings nicht viel erkennen. Sie fordern Opa Schulz auf, das Bild an der Wand so zu vergrößern, dass es doppelt so hoch ist. Wie weit entfernt muss Opa Schulz den Projektor von der Wand aufstellen?
Entfernung bestimmen
Um die doppelte Höhe des Bildes zu erreichen, streckst du die einzelnen Strecken mit dem Faktor 2:
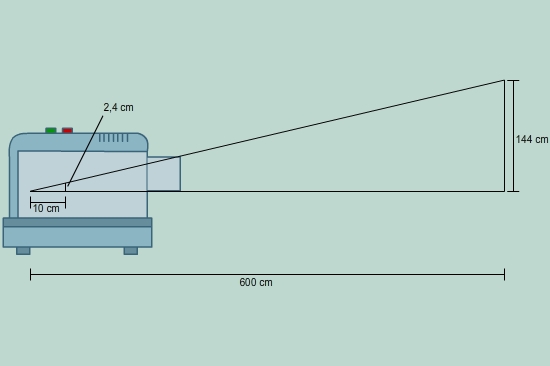 Damit das Bild an der Wand doppelt so groß ist wie zuvor, muss Opa Schulz den Projektor in doppelter Entfernung als zuvor zur Wand aufstellen
.
Damit das Bild an der Wand doppelt so groß ist wie zuvor, muss Opa Schulz den Projektor in doppelter Entfernung als zuvor zur Wand aufstellen
.
 Damit das Bild an der Wand doppelt so groß ist wie zuvor, muss Opa Schulz den Projektor in doppelter Entfernung als zuvor zur Wand aufstellen
.
Damit das Bild an der Wand doppelt so groß ist wie zuvor, muss Opa Schulz den Projektor in doppelter Entfernung als zuvor zur Wand aufstellen
.
Opa Schulz muss den Projektor
von der Wand entfernt aufstellen.
Der erste Strahlensatz
Im ersten Strahlensatz wird das Verhältnis der Strahlenabschnitte betrachtet.
Werden zwei Strahlen mit gemeinsamen Anfangspunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich je zwei Abschnitte auf dem einen Strahl wie die entsprechenden (gleichliegenden) Abschnitte auf dem anderen Strahl.
Es gilt:
und
und
 Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.
Es gilt:
und
und
Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.
Es gilt:
und
und
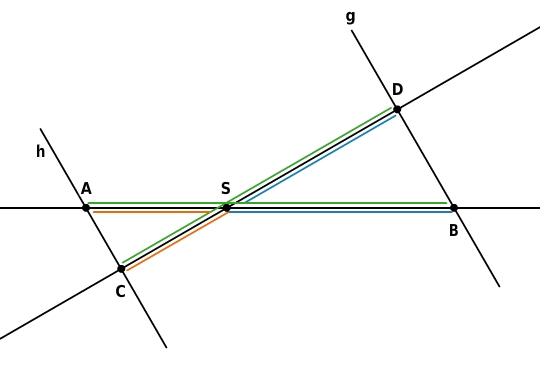 Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
 Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.
Es gilt:
und
und
Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen Geraden.
Es gilt:
und
und
 Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Markiere die Strecke in der Strahlensatzfigur nach dem ersten Strahlensatz in den entsprechenden Farben.
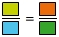
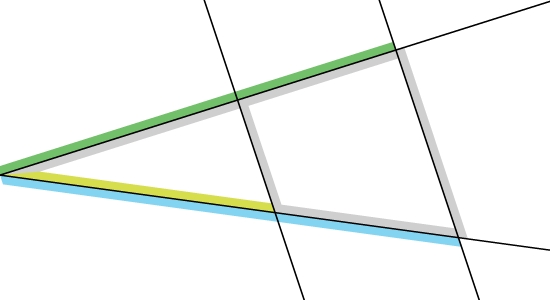


Strecke markieren
Für die Lösung verwendest du den ersten Strahlensatz.
Es gilt die Regel
"kurz zu lang wie kurz zu lang".
Auf dem unteren Strahl sind bereits zwei Abschnitte markiert (kurz zu lang = gelb zu blau).Auf dem oberen Strahl ist der lange Abschnitt grün und es fehlt noch der entsprechende kurze Abschnitt auf demselben Strahl in Orange.

Ergänze die Verhältnisgleichung nach dem ersten Strahlensatz.
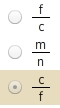

Verhältnisgleichung ergänzen
Für die Lösung verwendest du den ersten Strahlensatz.
Auf der einen Geraden sind bereits zwei Abschnitte gegeben (kurz zu lang =
).
Gesucht ist nun das Verhältnis zweier entsprechender Abschnitte auf der andern Geraden, also kurz zu lang =
.
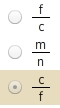
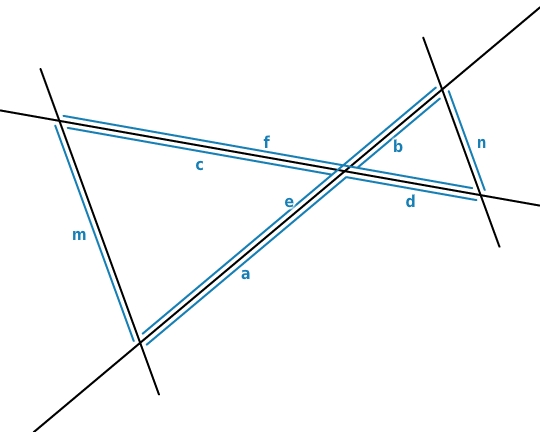
Vervollständige die Verhältnisgleichung, bei der die Längen a und d
e
f gegeben sind, nach dem ersten Strahlensatz.
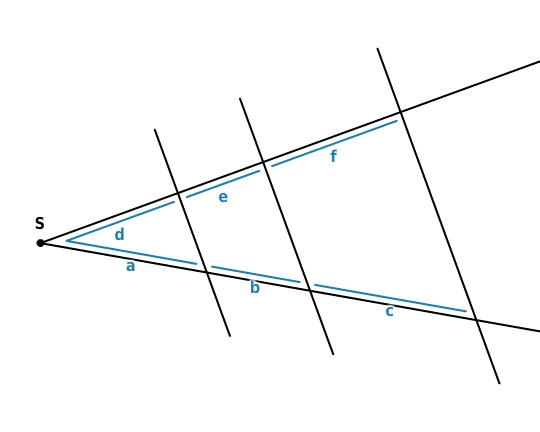

Verhältnisgleichung vervollständigen
Für die Lösung verwendest du den ersten Strahlensatz.
Es gilt die Regel:
"kurz zu lang wie kurz zu lang".
Auf dem unteren Strahl ist die Länge des kurzen Abschnitts gegeben (a), auf dem oberen die Länge des langen Abschnitts (d
e
f).
Es fehlt d
e
f entsprechend die Länge des langen Abschnitts auf dem unteren Strahl (a+b+c) und a entsprechend die Länge des kurzen Abschnitts auf dem oberen Strahl (d).
Der zweite Strahlensatz
Im zweiten Strahlensatz werden die Verhältnisse der Parallelenabschnitte und der Strahlenabschnitte betrachtet.
Werden zwei Strahlen mit gemeinsamen Anfangspunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jedem der Strahlen.
Es gilt:
und
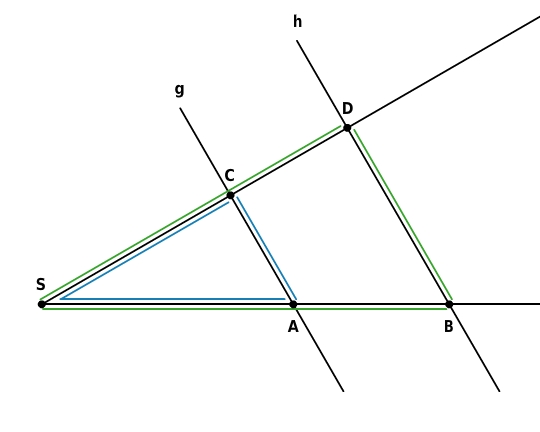 Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jeder der Geraden.
Es gilt:
und
Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jeder der Geraden.
Es gilt:
und
 Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
 Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jeder der Geraden.
Es gilt:
und
Diese Strahlensatzfigur wird wegen ihrer Form auch V-Figur genannt.
Werden zwei sich schneidende Geraden mit dem Schnittpunkt S von zwei parallelen Geraden g und h geschnitten, dann verhalten sich die Parallelenabschnitte wie die zugehörigen Abschnitte auf jeder der Geraden.
Es gilt:
und
 Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Diese Strahlensatzfigur wird wegen ihrer Form auch X-Figur genannt.
Markiere die Strecke in der Strahlensatzfigur nach dem zweiten Strahlensatz in den entsprechenden Farben.
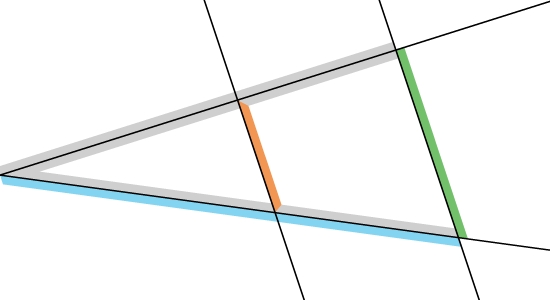


Strecke markieren
Für die Lösung verwendest du den zweiten Strahlensatz.
Es gilt die Regel:
"kurz zu lang wie kurz zu lang".
Die beiden Parallelenabschnitte sind bereits markiert (kurz/lang = orange/grün).
Auf dem unteren Strahl ist der lange Abschnitt in blau markiert, es fehlt noch der entsprechende kurze Abschnitt auf demselben Strahl in gelb.

Vervollständige die Verhältnisgleichung, bei der die Längen m und d gegeben sind, nach dem zweiten Strahlensatz.


Verhältnisgleichung vervollständigen
Für die Lösung verwendest du den zweiten Strahlensatz.
Der Parallelenabschnitt m und der Geradenabschnitt d sind bereits gegeben.
Es fehlen noch der zu m gehörende Geradenabschnitt derselben Geraden (c) und der zweite Parallelenabschnitt (n).
Ergänze die Verhältnisgleichung nach dem zweiten Strahlensatz.
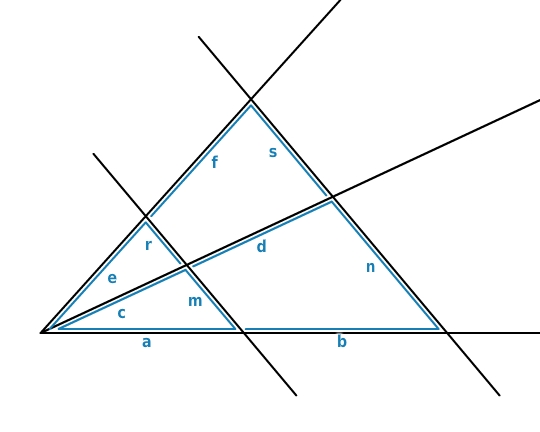

Verhältnisgleichung ergänzen
Für die Lösung verwendest du den zweiten Strahlensatz.
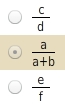
Das Verhältnis der Längen von zwei Parallelenabschnitten ist bereits gegeben kurz lang = r s .
Gesucht werden nun auf einem der Strahlen zwei Abschnitte, deren Längen im selben Verhältnis stehen a a+b .


