+49 30 300 2440 00
 – Mo bis Fr von 8:30 - 17 Uhr

Binomische Formeln

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, was binomische Formeln sind und wie du sie geschickt zum Lösen von Aufgaben verwenden kannst.Die binomischen Formeln beschreiben einen Spezialfall der Multiplikation von zwei Klammertermen.Das Wort „binomisch“ kommt aus dem Lateinischen von „bi“ + „nomen“ und bedeutet so viel wie „zwei Namen“, d. h. die Klammern enthalten genau zwei Summanden oder eine Differenz.Es gibt drei binomische Formeln:

Die erste binomische Formel

a + b 2 = a + b · a + b = a 2 + 2 a b + b 2 Die erste binomische Formel lässt sich durch ein Quadrat mit der Seitenlänge a + b darstellen.
/wp-content/uploads/media/kem_T_TPotBinF_1.jpg
Die Gesamtfläche A des Quadrats mit der Seitenlänge a + b setzt sich aus den Teilflächen a ?, a   b , b   a und b " zusammen.
  A = a + b 2   A = a + b a + b   A = a 2 + a b + b a + b 2   A = a 2 + a b + a b + b 2   A = a 2 + 2 a b + b 2
Löse im Term 3 + x 2 die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der ersten binomischen Formel mit a = 3 und b = x erhältst du:
/wp-content/uploads/media/kem_T_TPotBinF_2.jpg
9 + 6 x + x 2
Löse im Term 3 x + 2 y 2 die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der ersten binomischen Formel mit a = 3 x und b = 2 y erhältst du:
/wp-content/uploads/media/kem_T_TPotBinF_3.jpg
9 x 2 + 12 x y + 4 y 2
Forme den Term 25 x 2 + 30 x + 9 mit Hilfe der ersten binomischen Formel zu einem Produkt um.
Vereinfachen
Durch Anwendung der ersten binomischen Formel mit a = 5 x und b = 3 erhältst du:
/wp-content/uploads/media/kem_T_TPotBinF_4.jpg
Bei dieser Aufgabe wäre die Lösung -5 x - 3 2 ebenfalls richtig. Beide Summanden in der Klammer wurden mit (-1) multipliziert.
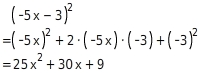/wp-content/uploads/media/kem_T_TPotBinF_5.jpg.
5 x + 3 2

Die zweite binomische Formel

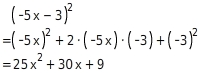a - b 2 = a - b · a - b = a 2 - 2 a b + b 2 Die zweite binomische Formel lässt sich über ein Quadrat mit der Seitenlänge a darstellen, die anschließend um b verkürzt wird.
  A = a - b 2   A = a - b a - b   A = a 2 - a b - b a + b 2   A = a 2 - a b - a b + b 2   A = a 2 - 2 a b + b 2
Löse im Term 5 - a 2 die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der zweiten binomischen Formel mit a = 5 und b = a erhältst du:
/wp-content/uploads/media/kem_T_TPotBinF_6.jpg
25 - 10 a + a 2
Löse im Term 7 m - 5 n 2 die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der zweiten binomischen Formel mit a = 7 m und b = 5 n erhältst du:
/wp-content/uploads/media/kem_T_TPotBinF_7.jpg
49 m 2 - 70 m n + 25 n 2
Forme den Term 36 x 2 - 24 x y + 4 y 2 mit Hilfe der zweiten binomischen Formel zu einem Produkt um.
Vereinfachen
Der Term lässt sich mit Hilfe der zweiten binomischen Formel zusammenfassen, denn der erste und dritte Summand sind jeweils Quadrate und es gilt:
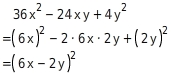
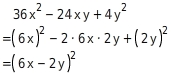
/wp-content/uploads/media/kem_T_TPotBinF_8.jpg
6 x - 2 y 2

Die dritte binomische Formel

a + b · a - b = a 2 - b 2 Die dritte binomische Formel lässt sich über ein Quadrat mit der Seitenlänge a darstellen, das anschließend an der einen Seite um b verlängert und an der anderen Seite um b verkürzt wird .
  A = a + b · a - b   A = a 2 + a b - b a - b 2   A = a 2 + a b - a b - b 2   A = a 2 - b 2
Löse im Term 7 + b · 7 - b die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der dritten binomischen Formel erhält man:
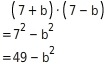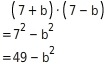/wp-content/uploads/media/kem_T_TPotBinF_9.jpg.
49 - b 2
Löse im Term -9 y - 5 z · -9 y + 5 z die Klammer auf und fasse so weit wie möglich zusammen.
Klammer auflösen
Durch Anwendung der dritten binomischen Formel erhält man:
/wp-content/uploads/media/kem_T_TPotBinF_10.jpg
81 y 2 - 25 z 2
Forme den Term 121 x 2 - 16 y 2 mit Hilfe der dritten binomischen Formel zu einem Produkt um.
Vereinfachen
/wp-content/uploads/media/kem_T_TPotBinF_11.jpg
11 x + 4 y · 11 x - 4 y