Beziehungen zwischen Winkeln
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren- Neben- und Scheitelwinkel an Geradenkreuzungen identifizieren
- Eigenschaften von Neben- und Scheitelwinkel an Geradenkreuzungen
- Neben- und Scheitelwinkel an Geradenkreuzungen berechnen
- Stufen- und Wechselwinkel an geschnittenen Parallelen identifizieren
- Eigenschaften von Neben-, Scheitel-, Stufen- und Wechselwinkeln an geschnittenen Parallelen
- Neben-, Scheitel-, Stufen- und Wechselwinkel an geschnittenen Parallelen berechnen
- Nebenwinkel mit Hilfe von Gleichungen berechnen
- Winkel an Doppelparallelen berechnen
- Winkel an komplexen Geradenkreuzungen berechnen
- Mehrere Winkel an komplexen Geradenkreuzungen berechnen
Neben- und Scheitelwinkel an Geradenkreuzungen identifizieren
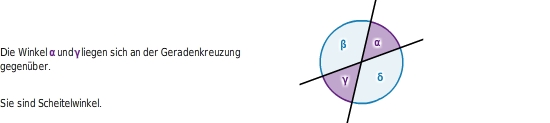
liegen einander gegenüber.
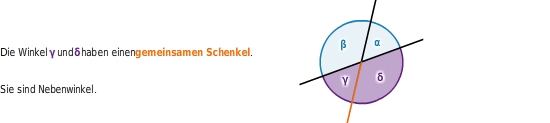
haben einen gemeinsamen
.
Eigenschaften von Neben- und Scheitelwinkel an Geradenkreuzungen
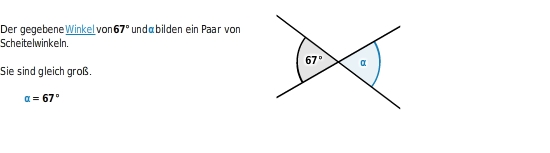
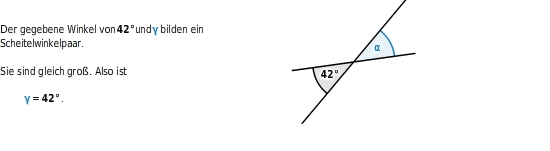
Scheitelwinkelsatz:
sind gleich groß.
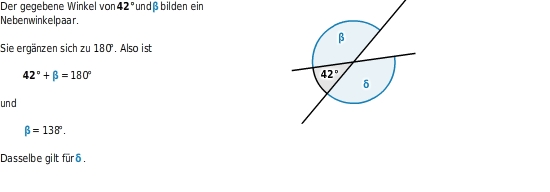
Nebenwinkelsatz:
ergänzen sie sich zu
.
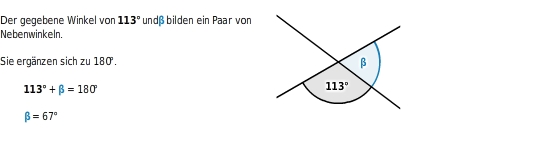
Neben- und Scheitelwinkel an Geradenkreuzungen berechnen
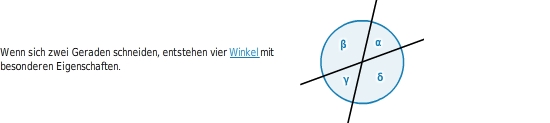
Schneiden sich zwei Geraden, entstehen vier
.
Ist dir einer dieser Winkel bekannt, kannst du alle anderen bestimmen.
Dabei nutzt du folgendes aus:

Stufen- und Wechselwinkel an geschnittenen Parallelen identifizieren
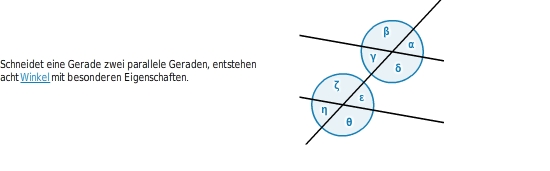
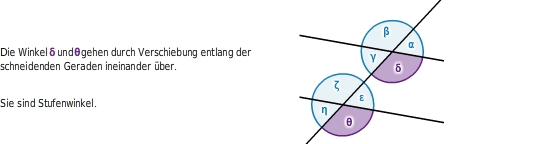
sind Winkel, die durch Verschiebung entlang der schneidenden Geraden ineinander übergehen.
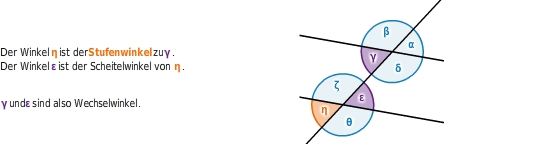
Der
zu einem gegebenen Winkel ist der
seines Stufenwinkels.
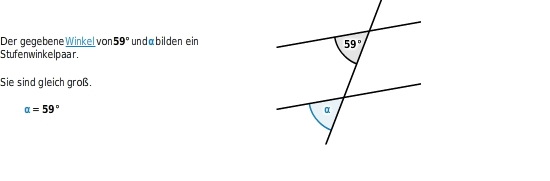
Eigenschaften von Neben-, Scheitel-, Stufen- und Wechselwinkeln an geschnittenen Parallelen
sind gleich groß.
sind gleich groß.
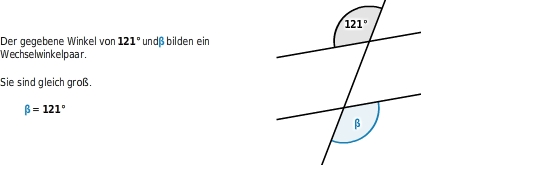
Neben-, Scheitel-, Stufen- und Wechselwinkel an geschnittenen Parallelen berechnen
Schneidet eine Gerade zwei parallele Geraden, entstehen acht
.
Ist dir einer dieser Winkel bekannt, kannst du alle anderen bestimmen.
Dabei nutzt du folgendes aus:
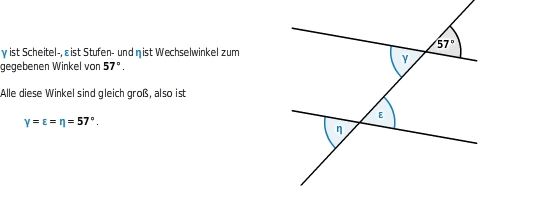
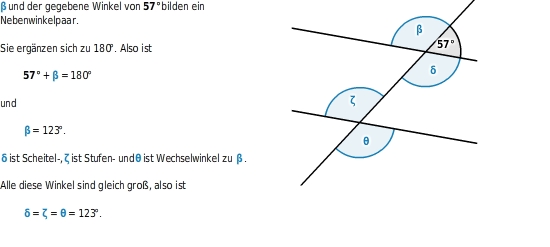
Nebenwinkel mit Hilfe von Gleichungen berechnen
Zwei
und
, die ein
bilden, ergänzen sich zu
.
Du kannst damit Aufgaben des folgenden Typs lösen.
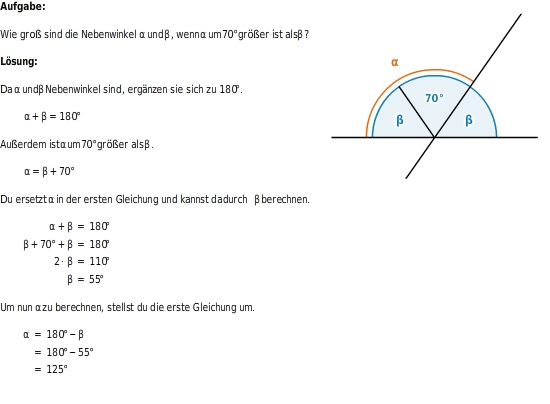
Winkel an Doppelparallelen berechnen
Kennst du einen
an zwei Parallelenpaaren, die sich schneiden, kannst du alle anderen Winkel über Winkelbeziehungen bestimmen.
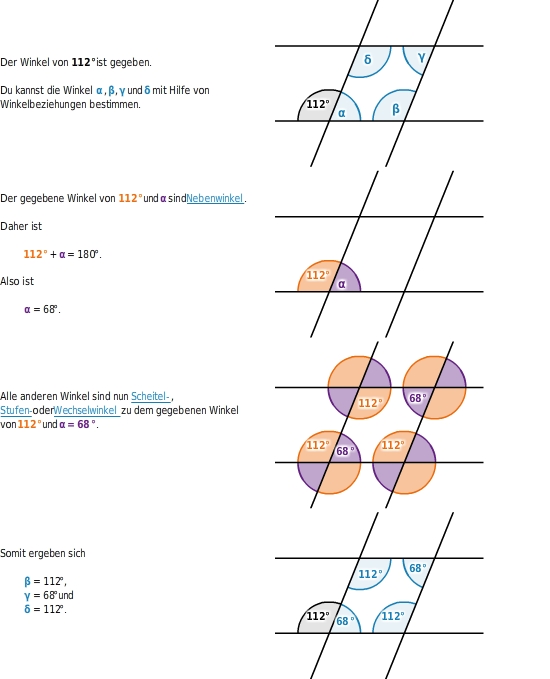
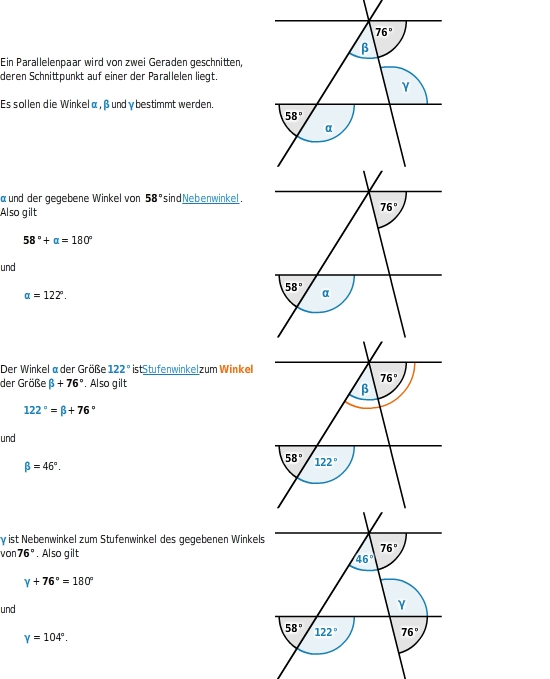
Winkel an komplexen Geradenkreuzungen berechnen
Auch wenn Parallelen von mehreren Geraden geschnitten werden, kannst du Winkelbeziehungen nutzen, um
zu bestimmen.
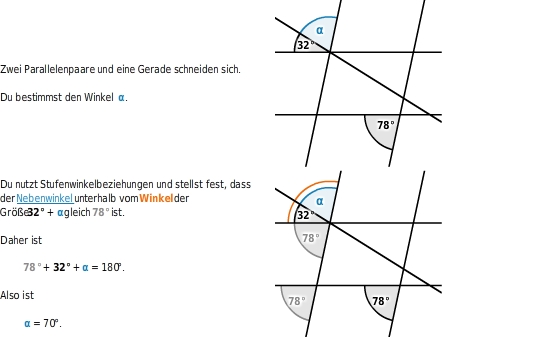
Mehrere Winkel an komplexen Geradenkreuzungen berechnen
Auch wenn Parallelen von mehreren Geraden geschnitten werden, kannst du Winkelbeziehungen nutzen, um
zu bestimmen.