bettermarks » Prüfungen am Ende der Jahrgangsstufe 10 » MSA Brandenburg » Terme und Gleichungen » Berechnen und Umformen von Termen

Berechnen und Umformen von Termen

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?

bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.

Mehr erfahren

Berechnen von Termwerten
Ausklammern in Termen mit Potenzen
Die erste binomische Formel
Die zweite binomische Formel
Die dritte binomische Formel
Terme aufstellen
Terme zu geometrischen Formen und Figuren
Multiplikation von Klammerausdrücken
Ausklammern

Berechnen von Termwerten

Viele Alltagssituationen (z. B. die monatliche Handyrechnung) oder geometrische Sachverhalte (Flächeninhalt eines Rechtecks) lassen sich durch Terme mit Variablen beschreiben. Um einen Termwert bestimmen zu können, musst du die Variablen durch Zahlenwerte ersetzen, die entweder durch die Alltagssituation vorgegeben sind oder die in einer Aufgabenstellung genannt werden. Nachdem du die Zahlenwerte für die Variablen eingesetzt hast, rechnest du den Term Schritt für Schritt aus.Wenn aber der Term z. B. verschiedene Rechenoperationen oder Klammern enthält, musst du die Rechenregel „Klammer- vor Punkt- vor Strichrechnung“ beachten.

Klammer- vor Punkt- vor Strichrechnung

Durch den Term

$0.09$

$x$

$+$

$0.15$

$y$

$+$

$9.95$ wird die monatliche Handyrechnung beschrieben, wobei eine Gesprächseinheit

$0.09 €$ kostet, eine SMS

$0.15 €$ und die Grundgebühr

$9.95 €$ beträgt. Für jede beliebige Anzahl von Gesprächseinheiten (x) und SMS (y) kann man nun den Rechnungsbetrag ermitteln.

Zum Beispiel:

Im letzten Monat wurden 56 Gesprächseinheiten und 32 SMS gezählt, also x = 56 und y = 32.

Einsetzen

Die Variablen x und y im Term 0,09x + 0,15y + 9,95 wurden durch die Zahlenwerte 56 und 32 ersetzt.

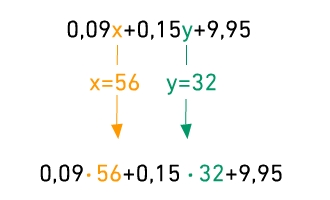/wp-content/uploads/media/kem_MSABB_MSABBTuGT_1.jpg

Zwischen den Koeffizienten und den eingesetzten Zahlenwerten muss das Multiplikationszeichen gesetzt werden.

$0.09$

$\cdot$

$56$

$+$

$0.15$

$\cdot$

$32$

$+$

$9.95$

Multiplizieren

Es gilt Punkt- vor Strichrechnung. Zunächst rechnest du also alle Produkte aus.Hier:

$0.09 \cdot 56 = 5.04$

$0.15 \cdot 32 = 4.80$

$5.04$

$+$

$4.80$

$+$

$9.95$

Addieren

Fasse im letzten Schritt alle Termglieder zusammen.

$5.04 + 4.80 + 9.95 = 19.79$ Bei einer Grundgebühr von

$9.95 €$ , 56 Gesprächsminuten zu

$0.09 €$ und 32 SMS zu

$0.15 €$ beträgt die Handyrechnung also

$19.79 €$ .

= 19,79

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_2.jpg

Durch den Term

$2$

$a$

$+$

$2$

$b$ wird der Umfang eines Rechtecks beschrieben. Für jede beliebige Länge (

$a$ ) und Breite (

$b$ ) eines Rechtecks kann man nun den Umfang des Rechtecks berechnen.

Zum Beispiel:

Berechne den Umfang eines Rechtecks mit den Seiten

$a$ =

$4$ cm und

$b$ =

$3$ cm.

Einsetzen

Die Variablen a und b im Term 2a + 2b wurden durch die Zahlenwerte 4 und 3 ersetzt.

$2$

$\cdot$

$4$

$+$

$2$

$\cdot$

$3$

Multiplizieren

Es gilt Punkt- vor Strichrechnung. Zunächst rechnest du also alle Produkte aus.Hier:

$2 \cdot 4 = 8$

$2 \cdot 3 = 6$

$8$

$+$

$6$

Addieren

Fasse im letzten Schritt alle Termglieder zusammen.

$8 + 6 = 14$ Ein Rechteck mit den Seitenlängen a =

$4 cm$ und b =

$3 cm$ hat den Umfang U =

$14 cm$ .

= 14

6 - x

$\cdot$ -8 + y

$-$

$5$ Berechne den Termwert für

$x$ =

$3$ und

$y$ =

$-2$

Einsetzen

Die Variablen x und y wurden durch die Werte 3 und (-2) ersetzt.

6 - 3

$\cdot$ -8 + (-2)

$-$

$5$

Klammern berechnen

Es gilt Klammer- vor Punkt- vor Strichrechnung.

$3$

$\cdot$ -10

$-$

$5$

Multiplizieren

Wegen Punkt- vor Strichrechnung berechnest du zunächst das Produkt

$3 \cdot (-10) = 30$ .

$-30$

$-$

$5$

Subtrahieren

= -35

Ausklammern in Termen mit Potenzen

Du kannst Koeffizienten (Zahlen) ausklammern, einzelne Variablen oder sogar ganze Terme, die als gemeinsame Faktoren in den Summanden vorkommen.

Um einen Koeffizienten ausklammern zu können, muss dieser als Faktor (d.h. als Teiler) unter allen Koeffizienten im Term vorkommen. Du kannst also stets den größten gemeinsamen Teiler (ggT) aller Koeffizienten ausklammern.

Klammere den größtmöglichen Faktor aus.

$9$

$x$

$+$

$12$

$y$

Ausklammern

Der größte gemeinsame Teiler von 9 und 12 ist 3.

$9 x : 3 = 3 x$

$12 y : 3 = 4 y$

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_4.jpg

Klammere so weit aus wie möglich.

$4$

$x^{2}$

$+$

$12$

$x$

$y$

$-$

$10$

$y$

$z^{2}$

$+$

$2$

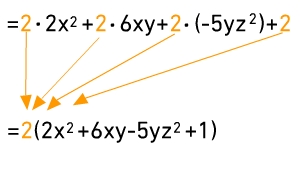
Ausklammern

Du kannst auch bei mehr als zwei Summanden ausklammern. Hier wurde bei allen vier Summanden der Faktor 2 ausgeklammert.Du erhältst die Terme in der Klammer, indem du jeden einzelnen Summanden des ursprünglichen Ausdrucks durch 2 dividierst. /wp-content/uploads/media/kem_MSABB_MSABBTuGT_5.jpg

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_5.jpg

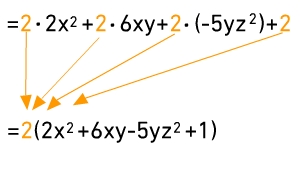
/wp-content/uploads/media/kem_MSABB_MSABBTuGT_6.jpg

Du kannst Koeffizienten und Variablen zusammen ausklammern, wenn der ausgeklammerte Term ein Teiler aller Summanden des ursprünglichen Terms ist.

Klammere so weit aus wie möglich.

$3$

$x^{2}$

$-$

$6$

$x$

$y$

Ausklammern

$3$

$x^{2}$ und -6xy enthalten beide die Faktoren 3 und x. Diese kannst du ausklammern.

$3$

$x$ x - 2 y

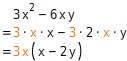
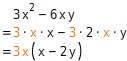
Klammere so weit aus wie möglich.

$6$

$x^{2}$

$+$

$12$

$x^{3}$

$y$

$-$

$14$

$x^{2}$

$z$

Ausklammern

Hier wurde bei allen vier Summanden der Faktor

$2$

$x^{2}$ ausgeklammert. /wp-content/uploads/media/kem_MSABB_MSABBTuGT_8.jpg

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_9.jpg

Die erste binomische Formel

${(a + b)}^{2} = (a + b) \cdot (a + b) = a^{2} + 2 a b + b^{2}$ Die erste binomische Formel lässt sich durch ein Quadrat mit der Seitenlänge

$a$

$+$

$b$ darstellen.

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_10.jpg

Die Gesamtfläche

$A$ des Quadrats mit der Seitenlänge

$a$

$+$

$b$ setzt sich aus den Teilflächen

$a$ ?,

$a$

$b$ ,

$b$

$a$ und

$b$ " zusammen.

$A = {(a + b)}^{2}$

$A = (a + b) (a + b)$

$A = a^{2} + a b + b a + b^{2}$

$A = a^{2} + a b + a b + b^{2}$

$A = a^{2} + 2 a b + b^{2}$

Löse im Term

${(3 + x)}^{2}$ die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der ersten binomischen Formel mit

$a = 3$ und

$b = x$ erhältst du:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_11.jpg

$9$

$+$

$6$

$x$

$+$

$x^{2}$

Löse im Term

${(3 x + 2 y)}^{2}$ die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der ersten binomischen Formel mit

$a = 3 x$ und

$b = 2 y$ erhältst du:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_12.jpg

$9$

$x^{2}$

$+$

$12$

$x$

$y$

$+$

$4$

$y^{2}$

Forme den Term

$25$

$x^{2}$

$+$

$30$

$x$

$+$

$9$ mit Hilfe der ersten binomischen Formel zu einem Produkt um.

Vereinfachen

Durch Anwendung der ersten binomischen Formel mit

$a = 5 x$ und

$b = 3$ erhältst du:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_13.jpg

Bei dieser Aufgabe wäre die Lösung

${(-5 x - 3)}^{2}$ ebenfalls richtig. Beide Summanden in der Klammer wurden mit (-1) multipliziert.

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_14.jpg

${(5 x + 3)}^{2}$

Die zweite binomische Formel

${(a - b)}^{2} = (a - b) \cdot (a - b) = a^{2} - 2 a b + b^{2}$ Die zweite binomische Formel lässt sich über ein Quadrat mit der Seitenlänge

$a$ darstellen, die anschließend um

$b$ verkürzt wird.

$A = {(a - b)}^{2}$

$A = (a - b) (a - b)$

$A = a^{2} - a b - b a + b^{2}$

$A = a^{2} - a b - a b + b^{2}$

$A = a^{2} - 2 a b + b^{2}$

Löse im Term

${(5 - a)}^{2}$ die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der zweiten binomischen Formel mit

$a = 5$ und

$b = a$ erhältst du:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_15.jpg

$25$

$-$

$10$

$a$

$+$

$a^{2}$

Löse im Term

${(7 m - 5 n)}^{2}$ die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der zweiten binomischen Formel mit

$a = 7 m$ und

$b = 5 n$ erhältst du:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_16.jpg

$49$

$m^{2}$

$-$

$70$

$m$

$n$

$+$

$25$

$n^{2}$

Forme den Term

$36$

$x^{2}$

$-$

$24$

$x$

$y$

$+$

$4$

$y^{2}$ mit Hilfe der zweiten binomischen Formel zu einem Produkt um.

Vereinfachen

Der Term lässt sich mit Hilfe der zweiten binomischen Formel zusammenfassen, denn der erste und dritte Summand sind jeweils Quadrate und es gilt:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_17.jpg

${(6 x - 2 y)}^{2}$

Die dritte binomische Formel

$(a + b) \cdot (a - b) = a^{2} - b^{2}$ Die dritte binomische Formel lässt sich über ein Quadrat mit der Seitenlänge

$a$ darstellen, das anschließend an der einen Seite um

$b$ verlängert und an der anderen Seite um

$b$ verkürzt wird .

$A = (a + b) \cdot (a - b)$

$A = a^{2} + a b - b a - b^{2}$

$A = a^{2} + a b - a b - b^{2}$

$A = a^{2} - b^{2}$

Löse im Term 7 + b

$\cdot$ 7 - b die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der dritten binomischen Formel erhält man:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_18.jpg

$49$

$-$

$b^{2}$

Löse im Term -9 y - 5 z

$\cdot$ -9 y + 5 z die Klammer auf und fasse so weit wie möglich zusammen.

Klammer auflösen

Durch Anwendung der dritten binomischen Formel erhält man:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_19.jpg

$81$

$y^{2}$

$-$

$25$

$z^{2}$

Forme den Term

$121$

$x^{2}$

$-$

$16$

$y^{2}$ mit Hilfe der dritten binomischen Formel zu einem Produkt um.

Vereinfachen

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_20.jpg

11 x + 4 y

$\cdot$ 11 x - 4 y

Terme aufstellen

Rechenanweisungen können mit Hilfe von Termen formuliert werden.Diese übersetzungshilfen können dir die Umwandlung erleichtern:

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_21.jpg

Formuliere den Term zu folgender Rechenanweisung.Vermindere das Siebenfache einer Zahl um 5 und dividiere das Ergebnis durch 2.

Term aufstellen

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_22.jpg

7 x - 5

$:$

$2$

Terme zu geometrischen Formen und Figuren

Bei ebenen Figuren lassen sich Umfang und Flächeninhalt mit Hilfe von Termen beschreiben.Ebenso bei Körpern das Volumen, der Oberflächeninhalt oder die Gesamtkantenlänge.

Umfang eines Rechtecks

Gib einen Term an, der den Umfang des Rechtecks mit den Seitenlängen a und b beschreibt. /wp-content/uploads/media/kem_MSABB_MSABBTuGT_23.jpg

Zur Erinnerung: Der Umfang eines Rechtecks ist die Summe der vier Seitenlängen.überlege zunächst, welche Seiten die gleiche Länge haben.

- Beim Rechteck sind gegenüber liegende Seiten gleich lang. - Für die Seitenlängen legst du eine Variable fest, z.B. nennst du die Länge der längeren Seite a und die der kürzeren Seite b

Term aufstellen

Da der Umfang die Summe aller Seitenlängen ist, addierst du die Seitenlängen.

$a + b + a + b = a + a + b + b$ Kommen Variablen mehrmals vor, kannst du sie zusammenfassen.

$2$

$\cdot$

$a$

$+$

$2$

$\cdot$

$b$ Multiplikationszeichen zwischen Zahl und Variable werden nicht notiert.

$2$

$a$

$+$

$2$

$b$

$2$

$a$

$+$

$2$

$b$

Gesamtkantenlänge eines Quaders

Gib einen Term an, der die Gesamtkantenlänge eines Quaders mit den Kantenlängen a, b und c beschreibt. /wp-content/uploads/media/kem_MSABB_MSABBTuGT_24.jpg

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_24.jpg

Zur Erinnerung: Die Gesamtkantenlänge ist die Summe aller Kantenlängen des Körpers. überlege zunächst, welche Kanten die gleiche Länge haben. - Da der Quader eine rechteckige Grundfläche hat, kommen dessen rot gezeichnete Länge (a) und dessen blau gezeichnete Breite (b) jeweils viermal vor. - Die grün gezeichnete Höhe (c) kommt ebenfalls viermal vor.

Term aufstellen

Da die Gesamtkantenlänge die Summe aller Kantenlängen ist, addierst du die Kantenlängen.

$4$

$a$

$+$

$4$

$b$

$+$

$4$

$c$

Multiplikation von Klammerausdrücken

Du kannst Summen — z.B. 3 x + 5 — bzw. Differenzen — z.B. 7 a - 2 a b — mit einem Term multiplizieren, indem du jedes einzelne Glied der Summe bzw. der Differenz mit diesem Term multiplizierst. Du wendest dabei das Distributivgesetz an.Terme können dabei Zahlen sein, aber auch Ausdrücke, die Variablen enthalten.

Multiplikation einer Summe / Differenz mit einer Zahl.

Löse die Klammer auf.

$3$

$\cdot$ a + 2 b

Ausmultiplizieren

$3$

$a$

$+$

$6$

$b$

Löse die Klammer auf. 3 a - 2 b

$\cdot$ -5

Ausmultiplizieren

$-15$

$a$

$+$

$10$

$b$

Multiplikation einer Summe / Differenz mit einem Term, der Variablen enthält.

Löse die Klammer auf.

$x$

$\cdot$ 2 x + y

Ausmultiplizieren

$2$

$x^{2}$

$+$

$x$

$y$

Löse die Klammer auf. 2 x y - x z

$\cdot$ -5 x 2

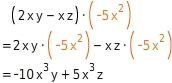
Ausmultiplizieren

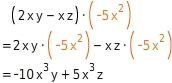
/wp-content/uploads/media/kem_MSABB_MSABBTuGT_29.jpg

$-10$

$x^{3}$

$y$

$+$

$5$

$x^{3}$

$z$

Ausklammern

Beim Ausklammern wird das Distributivgesetz „rückwärts“ angewendet.Wenn die Glieder einer Summe bzw. Differenz gleiche Faktoren enthalten, kannst du diese Summe bzw. Differenz in ein Produkt umwandeln. Du dividierst die einzelnen Glieder durch den gemeinsamen Faktor, klammerst die Summe bzw. Differenz der Ergebnisse ein und schreibst den gemeinsamen Faktor vor die Klammer.

/wp-content/uploads/media/kem_MSABB_MSABBTuGT_30.jpg

Um einen Koeffizienten (eine Zahl) ausklammern zu können, muss dieser als Faktor (d.h. als Teiler) in allen Koeffizienten im Term vorkommen. Du kannst also stets den größten gemeinsamen Teiler (ggT) aller Koeffizienten ausklammern.Beide Summanden enthalten im Beispiel den Faktor ggT (3;6) =

$3$ .Der Faktor

$3$ kann ausgeklammert werden.

Klammere so weit wie möglich aus.

$3$

$x^{2}$

$-$

$6$

$x$

$y$

Ausklammern

$3$

$x^{2}$ und

$-6$

$x$

$y$ enthalten beide die Faktoren 3 und x. Diese kannst du ausklammern.

$3$

$x$ x - 2 y

Berechnen und Umformen von Termen

Berechnen von Termwerten

Ausklammern in Termen mit Potenzen

Die erste binomische Formel

Die zweite binomische Formel

Die dritte binomische Formel

Terme aufstellen

Terme zu geometrischen Formen und Figuren

Multiplikation von Klammerausdrücken

Ausklammern

Produkte

Unternehmen

Service