Beispiele für Funktionen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier kannst du wichtige Beispiele für Funktionen kennenlernen.
Proportionale und antiproportionale Zuordnungen als Funktionen
Proportionale Zuordnungen sind spezielle Funktionen.
Die Zuordnungsvorschrift jeder proportionalen Zuordnung lässt sich immer in der Form
x  m x
schreiben, wobei m der Proportionalitätsfaktor ist.
Eine Funktion mit solch einer Zuordnungsvorschrift heißt proportionale Funktion.
m x
schreiben, wobei m der Proportionalitätsfaktor ist.
Eine Funktion mit solch einer Zuordnungsvorschrift heißt proportionale Funktion.
In der Wertetabelle ist eine proportionale Zuordnung gegeben.
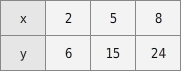
Eine proportionale Zuordnung erkennst du daran, dass für jedes Wertepaar der Quotient aus y-Wert und x-Wert gleich ist:
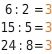 Für jedes Wertepaar (x;y) der Zuordnung gilt:
.Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Die Zahl 3 ist also der Proportionalitätsfaktor:
.
Die in der Wertetabelle angegebenen Wertepaare gehören somit zum Graphen der Funktion f mit
.
Für jedes Wertepaar (x;y) der Zuordnung gilt:
.Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Die Zahl 3 ist also der Proportionalitätsfaktor:
.
Die in der Wertetabelle angegebenen Wertepaare gehören somit zum Graphen der Funktion f mit
.
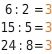 Für jedes Wertepaar (x;y) der Zuordnung gilt:
.Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Die Zahl 3 ist also der Proportionalitätsfaktor:
.
Die in der Wertetabelle angegebenen Wertepaare gehören somit zum Graphen der Funktion f mit
.
Für jedes Wertepaar (x;y) der Zuordnung gilt:
.Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Die Zahl 3 ist also der Proportionalitätsfaktor:
.
Die in der Wertetabelle angegebenen Wertepaare gehören somit zum Graphen der Funktion f mit
.
Du kannst eine proportionale Zuordnung – und damit eine proportionale Funktion – an ihrem Graphen erkennen.
Wenn du die Wertepaare einer proportionalen Zuordnung als Punkte in ein Koordinatensystem einträgst, liegen alle Punkte auf derselben Ursprungsgeraden.


Antiproportionale Zuordnungen sind – ebenso wie die proportionalen Zuordnungen – spezielle Funktionen.
Die Zuordnungsvorschrift einer antiproportionalen Zuordnung lässt sich immer in der Form
x  schreiben, wobei k eine von Null verschieden Zahl ist.
Eine Funktion mit solch einer Zuordnungsvorschrift heißt antiproportionale Funktion.
schreiben, wobei k eine von Null verschieden Zahl ist.
Eine Funktion mit solch einer Zuordnungsvorschrift heißt antiproportionale Funktion.
In der Wertetabelle ist eine antiproportionale Zuordnung gegeben.
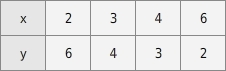

Eine antiproportionale Zuordnung erkennst du daran, dass für jedes Wertepaar das Produkt aus x- und y-Wert dieselbe von Null verschiedene Zahl ergibt:
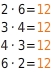 Für jedes Wertepaar (x; y) der Zuordnung gilt:
.
Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Für jedes Wertepaar (x; y) der Zuordnung gilt:
.
Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
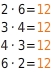 Für jedes Wertepaar (x; y) der Zuordnung gilt:
.
Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Für jedes Wertepaar (x; y) der Zuordnung gilt:
.
Daraus erhältst du die Zuordnungsvorschrift, indem du die Gleichung nach y umstellst:
.
Die in der Wertetabelle angegebenen Wertepaare gehören somit zum Graphen der Funktion f mit
.

Antiproportionale Funktionen haben typische Graphen.
Wenn du die Wertepaare einer antiproportionalen Zuordnung als Punkte in ein Koordinatensystem einträgst, liegen alle Punkte auf dem Graphen derselben antiproportionalen Funktion mit einer Funktionsgleichung der Form
.
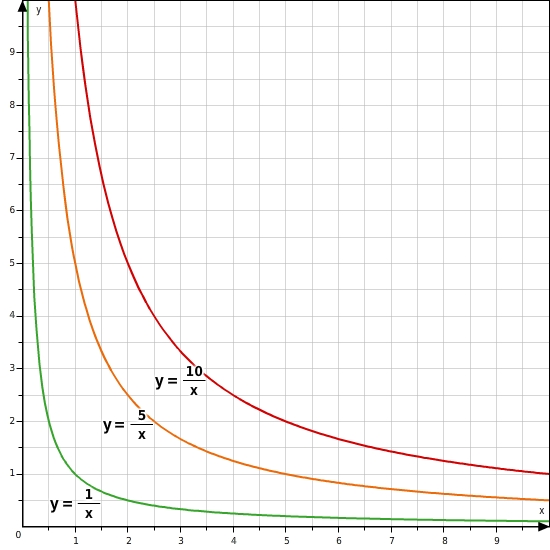
Der Graph jeder antiproportionalen Funktion heißt Hyperbel.
Im Bild sind die Graphen verschiedener antiproportionaler Funktionen für positive x-Werte dargestellt.

Lineare Funktionen kennenlernen
Der Graph einer proportionalen Funktion
ist eine Gerade durch den Ursprung. Umgekehrt ist jede Gerade durch den Koordinatenursprung, die nicht gleich der y-Achse ist, der Graph einer proportionalen Funktion.
Wenn du den Graphen einer proportionalen Funktion entlang der y-Achse parallel verschiebst, erhältst du wieder eine Gerade, die jedoch nicht durch den Ursprung verläuft.


Im Allgemeinen gilt:
Jede Gerade im Koordinatensystem, die nicht parallel zur y-Achse ist, ist der Graph einer Funktion mit einer Funktionsgleichung der Form
.
Funktionen mit solch einer Funktionsgleichung werden lineare Funktionen genannt.
Ein positives b entspricht einer Verschiebung des Graphen der proportionalen Funktion
entlang der y-Achse nach oben.
Ein negatives b entspricht einer Verschiebung des Graphen der proportionalen Funktion
entlang der y-Achse nach unten.
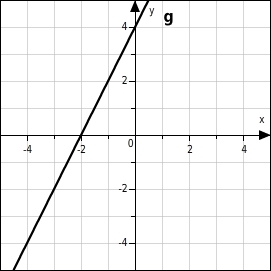
Interpretiere diesen Funktionsgraphen und ermittle die zugehörige Funktionsgleichung.

Graphen interpretieren
Da diese Gerade nicht durch den Koordinatenursprung verläuft, liegt hier keine proportionale Funktion vor.
Ist die abgebildete Gerade der Graph einer proportionalen Funktion?

Funktionsgleichung bestimmen
Du brauchst nur den Schnittpunkt des Graphen mit der
-Achse zu betrachten um zu erkennen, dass dem Argument 0 die Zahl 4 zugeordnet wird.
Du wählst also die Funktionsgleichung mit
aus:
Gib nun die Funktionsgleichung zu diesem Graphen an.
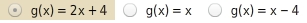
In welchen Farben sind die Graphen der linearen Funktionen dargestellt?



Lineare Funktionen erkennen
Jede Funktion, deren Graph einer Geraden entspricht, ist eine lineare Funktion.
Umgekehrt liegen bei jeder linearen Funktion die Punkte des Graphen auf einer Geraden. Du brauchst also lediglich zu überprüfen, welche der drei Geraden überhaupt Funktionen darstellen:
Die zur y-Achse parallele Gerade stellt keine Funktion dar, weil hier alle Zahlen der Zahl 3 zugeordnet werden. Diese Zuordnung ist nicht eindeutig.
Die anderen beiden Geraden sind Funktionen, weil es bei ihnen keine zwei Punkte auf dem Graphen gibt, die entlang einer Parallelen zur y-Achse übereinander liegen.
Lineare, antiproportionale und quadratische Funktionen im Vergleich
Alle Graphen linearer Funktionen y = f(x) = mx + b sind Geraden. Die Graphen antiproportionaler Funktionen y = f(x) = k x sind immer Hyperbeln.
In vielen Fällen sind die Graphen von Funktionen mit gleichartigen Funktionstermen bestimmte geometrische Figuren.
Eine weitere Sorte von Funktionen, deren Graphen eine typische geometrische Form haben, sind die so genannten quadratischen Funktionen.
Beispiele für quadratische Funktionen sind:
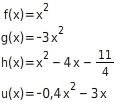

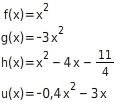

Eine quadratische Funktion ist eine Funktion, deren Funktionsterm die Summe oder Differenz aus einem von Null verschiedenen quadratischen Term a
und einem linearen Funktionsterm ist. Dieser lineare Funktionsterm kann auch gleich einer Konstanten oder gleich Null sein.
Der Graph einer jeden quadratischen Funktion ist eine Parabel.
Welche Zuordnungsvorschrift gehört zu einer quadratischen Funktion?
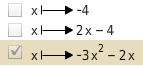
Funktionstyp erkennen
Der Funktionsterm der Zuordnungsvorschrift
 ist die Differenz aus dem quadratischen Term
und dem linearen Term
.
Somit gehört diese Zuordnungsvorschrift zu einer quadratischen Funktion.
ist die Differenz aus dem quadratischen Term
und dem linearen Term
.
Somit gehört diese Zuordnungsvorschrift zu einer quadratischen Funktion.
Ordne den Graphen die passenden Bezeichnungen und Funktionsterme zu.




Funktionen benennen
An der Form des Graphen kannst du erkennen, zu welchem der drei Funktionstypen (linear, antiproportional, quadratisch) der jeweilige Graph gehört.
Der Graph einer linearen Funktion ist eine Gerade.
Der Graph einer antiproportionalen Funktion ist eine Hyperbel.
Der Graph einer quadratischen Funktion ist eine Parabel.

Funktionsterme zuordnen
An der Form des Funktionsterms kannst du erkennen, welcher Funktionsterm zu welcher Funktion, und somit zu welchem Graphen gehört.
Die Funktionsgleichung der linearen Funktion hat die Form
.
Die Funktionsgleichung der antiproportionalen Funktion hat die Form
.
Die Funktionsgleichung der quadratischen Funktion hat die Form
.

Definitionslücken bei Funktionstermen
Zu einer Funktion gehört immer ein Definitionsbereich. Wenn eine Funktion durch einen Funktionsterm f(x) angegeben ist, darf ihr Definitionsbereich nur x-Werte enthalten, für die der Funktionswert f(x) berechnet werden kann.
Bei linearen und quadratischen Funktionen, also Funktionen mit einem Funktionsterm der Form
bzw.
, kann der Funktionswert für jeden x-Wert berechnet werden.
Man sagt, dass diese Funktionen für jeden beliebigen x-Wert definiert bzw. überall definiert sind.
Daher kann jede Menge von rationalen Zahlen der Definitionsbereich einer linearen bzw. quadratischen Funktion sein.
Die Funktion mit der Funktionsgleichung
ist überall definiert, da für jeden x-Wert der Funktionswert berechnet werden kann.
Es können daher zum Beispiel folgende Mengen als Definitionsbereich der Funktion f gewählt werden:


Bei antiproportionale Funktionen, also Funktionen mit einem Funktionsterm der Form
mit von Null verschiedenem k, kann der Funktionswert für
nicht berechnet werden, da durch Null nicht dividiert werden kann.
Somit gehört die Null nicht zum Definitionsbereich einer antiproportionalen Funktion.
Man sagt, dass antiproportionale Funktionen eine Definitionslücke an der Stelle Null haben.
Gegeben ist eine Funktion mit der Funktionsgleichung
.
Welche Mengen sind als Definitionsbereich der Funktion möglich?

Definitionsbereiche angeben
Die Funktion
ist eine antiproportionale Funktion. Sie hat bei Null eine Definitionslücke, da durch Null nicht dividiert werden kann.
Für alle anderen x-Werte kann der Funktionswert berechnet werden.
Daher kann jede Menge rationaler Zahlen, die nicht die Null enthält, ein Definitionsbereich der Funktion f sein.

Nullstellen bestimmen
In vielen Anwendungen haben die Nullstellen einer Funktion eine besondere Bedeutung.
An einer Nullstelle hat eine Funktion den Wert Null.
Wenn die Funktion f die Funktionsgleichung
hat, sind die Nullstellen alle x-Werte, für die
ist.

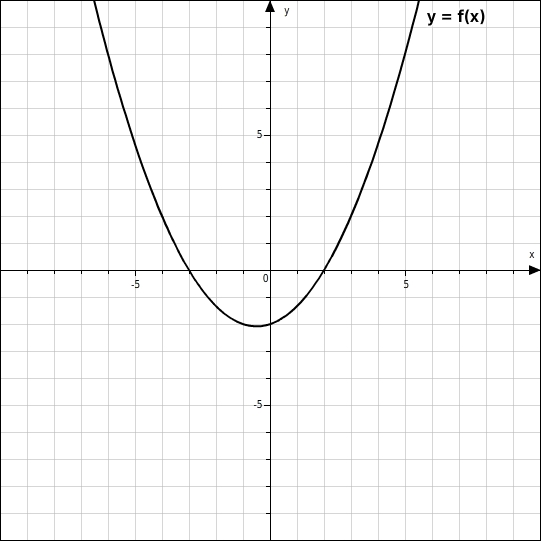
Die Nullstellen sind die x-Koordinaten der Schnittpunkte des Funktionsgraphen mit der x-Achse.
Welches Argument ist eine Nullstelle der Funktion f mit
?

Funktionswerte vergleichen
Du setzt die Argumente nacheinander für x in den Funktionsterm ein und rechnest aus:
 ist eine Nullstelle der Funktion f.
ist eine Nullstelle der Funktion f.
 ist eine Nullstelle der Funktion f.
ist eine Nullstelle der Funktion f.

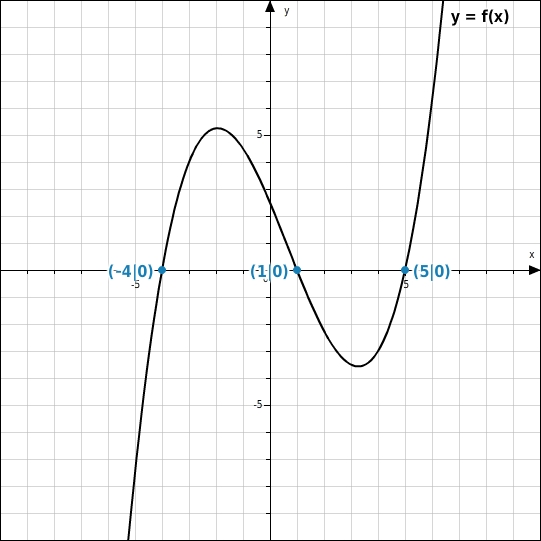
Bestimme mit Hilfe des Funktionsgraphen alle Nullstellen der Funktion f.


Nullstellen bestimmen
Der Graph der Funktion f schneidet die x-Achse an den Nullstellen. Du entnimmst dem Graphen, dass diese Schnittpunkte an den Stellen x = -3 und x = 2 liegen.




