Anwendungen
Online Mathe üben mit bettermarks
- Über 2.400 Übungen mit fast 200.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Hier erfährst du, wie du Textaufgaben mit Hilfe der Strahlensätze lösen und wie du konstruktiv eine Strecke in gleich lange Teilstrecken zerlegen kannst.
Lösen von Anwendungsaufgaben Schritt für Schritt
Textaufgaben lassen sich leichter lösen, wenn du Schritt für Schritt vorgehst.
Höhenbestimmung mit Hilfe der Schattenlänge
Die Laterne vor Lauras Fenster wirft einen
langen Schatten. Zur gleichen Zeit ist Lauras Schatten
lang. Laura selbst ist
groß.Wie hoch ist die Laterne?
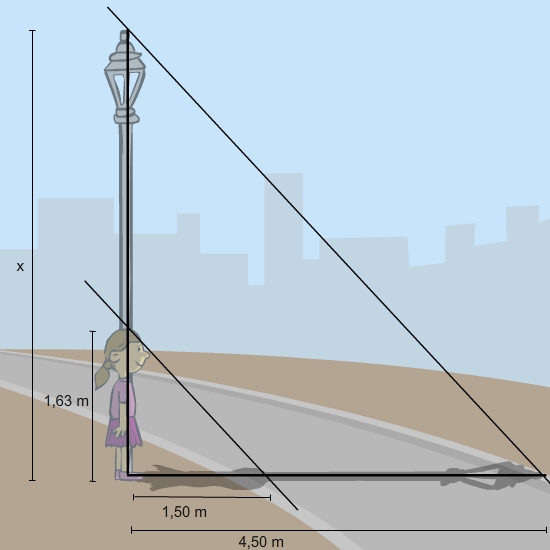
Skizze zum Sachverhalt
Wenn sich Laura direkt neben die Laterne stellt, entsteht aus Laterne, Laura und deren Schatten die Strahlensatzfigur in V-Form.
Verhältnisgleichung aufstellen
Du verwendest den ersten Strahlensatz. Die Laterne (
) und Laura (
) bilden die Abschnitte auf dem einen Strahl.Deren Schatten (
und
) sind die entsprechenden Abschnitte auf dem anderen Strahl.
Verhältnisgleichung lösen
Die Laterne ist etwa
hoch.
≈
Vermessungen im Gelände mit Messinstrumenten
Ein Försterdreieck ist ein Dreieck, das für die Bestimmung von Baumhöhen benutzt wird. Natürlich kannst du es auch für die Höhenbestimmung anderer Objekte benutzen.Du peilst über das Dreieck hinweg die Spitze des Baumes an, so dass das Dreieck gerade die Baumspitze verdeckt.Verwende folgende Längenangaben:
m;
m;
m;
m;Wie hoch ist der Baum?
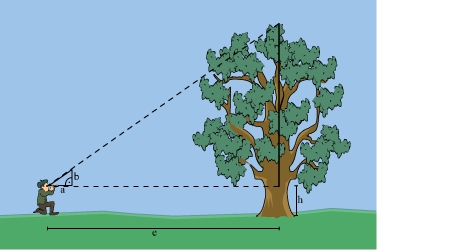
Skizze zum Sachverhalt
Die Entfernung zum Baum ist auf Augenhöhe dieselbe wie auf dem Boden. Es entsteht eine V-Figur.
Verhältnisgleichungen aufstellen
Du rechnest alle Angaben in die gleiche Einheit um und verwendest den zweiten Strahlensatz.
Verhältnisgleichung lösen
Höhe des Baumes berechnen
Um die Höhe des Baumes zu ermitteln, addierst du noch die Augenhöhe:
Der Baum ist
hoch.
Entfernungen schätzen mit Daumensprung
Du peilst abwechselnd mit dem linken und dem rechten Auge deinen Daumen über deinen ausgestreckten Arm an. Durch den Abstand zwischen deinen Augen erscheint dein Daumen einmal weiter links und einmal weiter rechts im Bild. Du kannst die ungefähre Entfernung zum Gegenstand berechnen, wenn du seine ungefähre Breite kennst.
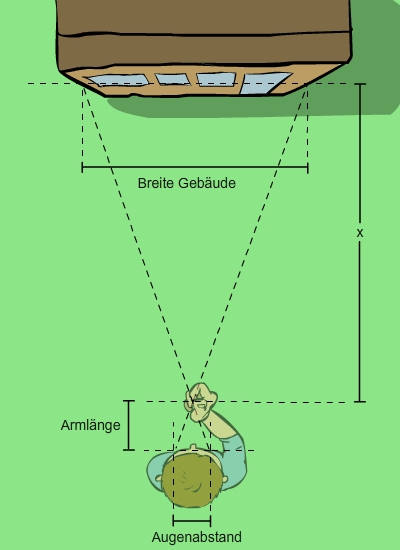
Pauls Augenabstand beträgt
, seine Armlänge
. Er schätzt die Breite des Gebäudes anhand der davor parkenden Autos auf
.Wie weit ist Paul ungefähr vom Gebäude entfernt?
Pauls Augenabstand beträgt
, seine Armlänge
. Er schätzt die Breite des Gebäudes anhand der davor parkenden Autos auf
.Wie weit ist Paul ungefähr vom Gebäude entfernt?
Skizze zum Sachverhalt
Pauls Augenabstand und die Breite des Gebäudes bilden die Parallelen in einer X-Figur. Den Schnittpunkt S der Geraden bildet Pauls Daumen.
Verhältnisgleichung aufstellen
Du rechnest alle Angaben in die gleiche Einheit um und verwendest den zweiten Strahlensatz.
Verhältnisgleichung lösen
= 385,
Da Paul die Breite des Gebäudes nur geschätzt hat, genügt es, für das Ergebnis einen stark gerundeten Wert anzugeben.Paul befindet sich ungefähr
vom Gebäude entfernt.
≈
Strecken teilen
Mit Hilfe der Strahlensätze kannst du eine Strecke in gleichgroße Abschnitte teilen, ohne die Länge der Strecke zu messen.Du kannst die Strecke auch in einem bestimmten Verhältnis teilen.
Teile die Strecke
in sieben gleich lange Strecken.
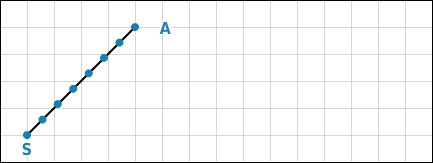
Strecke teilen
Du zeichnest einen Strahl mit dem Anfangspunkt S. Auf diesem trägst du vom Punkt S aus sieben gleich lange Teile ab.
Den Endpunkt des letzten Abschnittes verbindest du mit dem Punkt A.Nun zeichnest du durch die Teilstriche auf dem Strahl jeweils eine Parallele, die die Strecke
schneidet. Auf diese Weise entstehen auf der Strecke
ebenfalls sieben gleichgroße Abschnitte.
Den Endpunkt des letzten Abschnittes verbindest du mit dem Punkt A.Nun zeichnest du durch die Teilstriche auf dem Strahl jeweils eine Parallele, die die Strecke
schneidet. Auf diese Weise entstehen auf der Strecke
ebenfalls sieben gleichgroße Abschnitte.
Teile die Strecke
im Verhältnis 4:5.
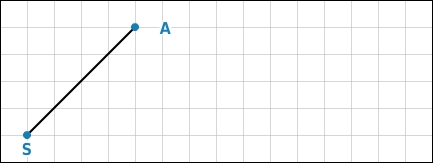
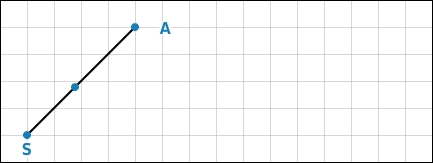
Strecke teilen
Du zeichnest einen Strahl mit dem Anfangspunkt S.Auf diesem trägst du vom Punkt S aus neun (4 + 5 = 9) gleich lange Teile ab.
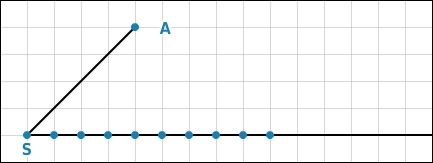Den Endpunkt des letzten Abschnittes verbindest du mit dem Punkt A.Nun zeichnest du durch den vierten Teilstrich eine Parallele, die die Strecke
schneidet. Auf diese Weise wird die Strecke
im Verhältnis 4 : 5 geteilt.
Den Endpunkt des letzten Abschnittes verbindest du mit dem Punkt A.Nun zeichnest du durch den vierten Teilstrich eine Parallele, die die Strecke
schneidet. Auf diese Weise wird die Strecke
im Verhältnis 4 : 5 geteilt.