Anwendungen von Exponentialfunktionen
Online Mathe üben mit bettermarks
- Über 2.400 Übungen mit fast 200.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Exponentialfunktionen mit prozentualer Zu- oder Abnahme
Nimmt eine Größe G ausgehend vom Anfangswert
pro Schritt um
zu bzw. ab, so kann ihr Wert in Abhängigkeit von der Anzahl x der Schritte mit einer
beschrieben werden:
bzw.
In einem Land wächst die Bevölkerung jährlich um
.
Derzeit leben
Mio. Menschen in diesem Land.
Das Bevölkerungswachstum kann beschrieben werden mit der
:
Nach 3 Jahren ist die Bevölkerung auf etwa 46 Mio. angewachsen.
Allgemeine Exponentialfunktion:
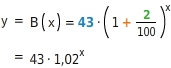In 3 Jahren:
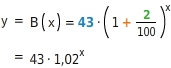In 3 Jahren:
Von der Verdopplungszeit zur Exponentialfunktion
Sind Anfangswert
und Verdopplungszeit T einer Größe G gegeben, so beschreibt der
den Wert der Größe G in Abhängigkeit von der Zeit x.
Eine Bakterienart vermehrt sich unter günstigen Bedingungen alle 40 Minuten durch Teilung. Das heißt, die Anzahl A der Bakterien verdoppelt sich in dieser Zeit.
Befinden sich anfangs 100 Bakterien in einer Petrischale, dann sind es nach 90 Minuten 476 Bakterien.
Von der Halbwertszeit zur Exponentialfunktion
Sind Anfangswert
und Halbwertszeit T einer Größe G gegeben, so beschreibt der
den Wert der Größe G in Abhängigkeit von der Zeit x.
Radioaktives Jod 131 hat eine
von 8 Tagen.
Befinden sich in einer Probe anfangs 45 mg Jod 131, dann sind nach 3 Tagen noch etwa 35 mg enthalten.
Exponentialfunktion aus Wertepaaren modellieren
Kennst du von einer
Größe die Werte
und
zu zwei verschiedenen Zeitpunkten
und
, dann kannst du eine
der Form
eindeutig finden, die dieses Wachstum beschreibt.
Um die Werte der Parameter a und b zu bestimmen, setzt du beide Wertepaare x 1 ; y 1 bzw. x 2 ; y 2 in die
ein und löst das dadurch entstandene
.
Für die Wertepaare 0 ; 9 und 3 ; 72 ergibt sich die Funktion
Gleichungssystem:
