Zusammengesetzte und ausgehöhlte Körper
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenAlle Formeln auf einen Blick
Würfel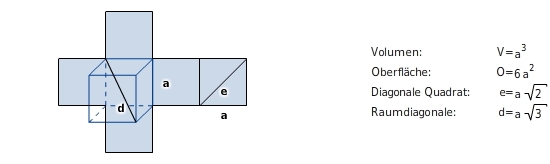
Quader
Prisma
Zylinder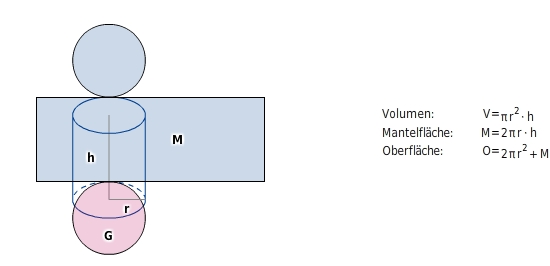
Pyramide
Kegel
Kugel
Berechnungen an zusammengesetzten Körpern
Ein zusammengesetzter Körper besteht aus zwei oder mehreren Teilkörpern.Das Volumen des zusammengesetzten Körpers ist die Summe der Volumen aller Teilkörper.Die Oberfläche ist die aller begrenzenden Teilflächen.
Beachte, dass die Flächen an denen sich die Körper berühren, nicht zur Oberfläche gehören.
Du gehst Schritt für Schritt vor: 
Volumenberechnung (Maße in m)
1.Teilkörper: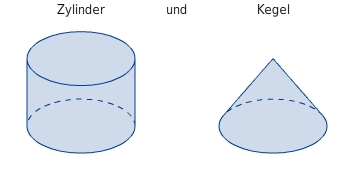
2. Formeln:
Rundungsfehler beim Rechnen bleiben klein, wenn du zuerst zusammenfasst und möglichst spät, bzw. erst am Ende mit .
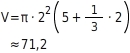
Berechnungen an ausgehöhlten Körpern
Ein ausgehöhlter Körper entsteht, indem du aus einem Körper einen oder mehrere andere Körper herausschneidest. Das Volumen des ausgehöhlten Körpers ist also kleiner als das des Grundkörpers ( ). Die Oberfläche ist größer als die des Grundkörpers, denn es kommen Teilflächen hinzu ( ). Du gehst Schritt für Schritt vor. 
Oberflächenberechnung (Maße in cm)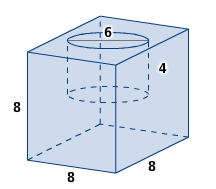
1. Teilfläche:
Die Grundfläche des Zylinders kommt zur Gesamtoberfläche hinzu, gleichzeitig wird eine ebenso große Kreisfläche von der Oberfläche des Würfels .
Rundungsfehler beim Rechnen bleiben klein, wenn du zuerst zusammenfasst und möglichst spät, bzw. erst am Ende mit .
