Zinseszins
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenFeste Verzinsung und Zinseszins
Von Zinseszins spricht man, wenn ein Geldbetrag (das Kapital) verzinst wird und die anfallenden Zinsen nach ihrer Gutschrift mit verzinst werden.
Wird ein Kapital mit einem festen Zinssatz von
p.a. und Zinseszins angelegt, so wächst das Kapital exponentiell und jährlich mit dem Zinsfaktor
Willst du die Größe eines über mehrere Jahre mit Zinseszins fest verzinsten Kapitals berechnen, verwendest du Potenzen des
b.
Hat das Kapital den Anfangswert
, dann gilt für den Wert
(nach n Jahren):
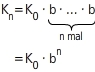
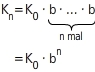
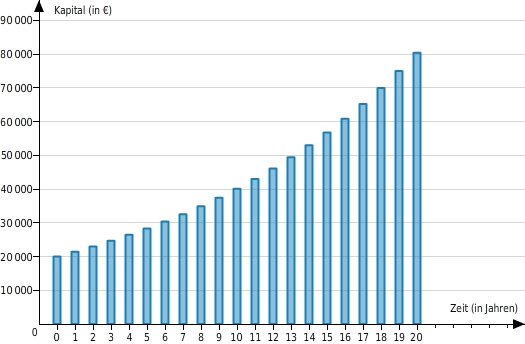
Ein Kapital von
wird zu einem Zinssatz von
p.a. über 20 Jahre fest angelegt.



Umgekehrt kannst du das Anfangskapital
und den von der Bank gebotenen Zinssatz p (in %) berechnen:
 und
mit
und
mit
Rendite bei variablem Zinssatz
Es gibt Anlageformen, bei denen der jährliche Zinssatz nicht konstant ist.
Der Faktor k, mit dem das Kapital dann insgesamt wächst, ist das Produkt der einzelnen Zinsfaktoren.
Um solche Anlagen mit anderen vergleichbar zu machen, wird der feste jährliche Zinssatz p, auch Rendite genannt, berechnet, mit dem das Kapital wachsen müsste, um denselben Ertrag zu erzielen.


Sparplan mit
Rendite
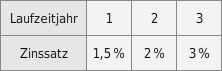
 Also:
Also:

 Also:
Also:

