Wurzellängen und Abstandsbestimmung im Koordinatensystem
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du eine Strecke konstruieren kannst, deren Länge gleich einem vorgegebenen Wurzelausdruck ist, und wie du den Abstand zwischen zwei Punkten im Koordinatensystem berechnen kannst.
Geometrische Darstellung von Quadratwurzeln
Die Wurzel einer natürlichen Zahl ist meistens eine
, z.B.
,
,
,
, ... Dennoch lassen sich diese Zahlen geometrisch als Längen von Strecken darstellen. Zum Beispiel hat die Diagonale in einem
die Länge
. Dies folgt aus dem Satz des Pythagoras.
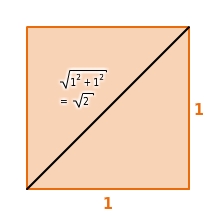

Auf ähnliche Weise lässt sich jede irrationale Zahl der Form
(n natürliche Zahl) als Länge einer Strecke konstruieren.
Diagonale im Quadrat
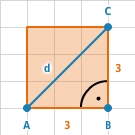 Die Diagonale ist die Hypotenuse in dem rechtwinkligen Dreieck
. Länge d der Diagonale: Nach dem Satz des Pythagoras gilt:
Die Diagonale ist die Hypotenuse in dem rechtwinkligen Dreieck
. Länge d der Diagonale: Nach dem Satz des Pythagoras gilt: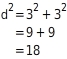 Also:
Also: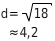
 Die Diagonale ist die Hypotenuse in dem rechtwinkligen Dreieck
. Länge d der Diagonale: Nach dem Satz des Pythagoras gilt:
Die Diagonale ist die Hypotenuse in dem rechtwinkligen Dreieck
. Länge d der Diagonale: Nach dem Satz des Pythagoras gilt: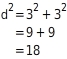 Also:
Also:
Konstruktion einer irrationalen Länge
Die Strecke
hat eine Länge von
.
 Du zeichnest ein rechtwinkliges Dreieck
, in dem
die Hypotenuse ist und die Länge
besitzt. Hierzu zerlegst du 40 in die Summe zweier Quadratzahlen:
Du zeichnest ein rechtwinkliges Dreieck
, in dem
die Hypotenuse ist und die Länge
besitzt. Hierzu zerlegst du 40 in die Summe zweier Quadratzahlen:
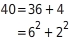 Du trägst 6 und 2 Kästchenlängen rechtwinklig im Raster ab und erhältst die Katheten
und
. Dann verbindest du die Punkte A und B.
Du trägst 6 und 2 Kästchenlängen rechtwinklig im Raster ab und erhältst die Katheten
und
. Dann verbindest du die Punkte A und B.
 Du zeichnest ein rechtwinkliges Dreieck
, in dem
die Hypotenuse ist und die Länge
besitzt. Hierzu zerlegst du 40 in die Summe zweier Quadratzahlen:
Du zeichnest ein rechtwinkliges Dreieck
, in dem
die Hypotenuse ist und die Länge
besitzt. Hierzu zerlegst du 40 in die Summe zweier Quadratzahlen:
Die Strecke mit der Länge
war einfach zu konstruieren, weil 40 die Summe zweier Quadratzahlen ist. Dies ist aber nicht für jede natürliche Zahl der Fall.
Beim Versuch, der Reihe nach Strecken der Längen
,
,
, ... zu konstruieren, wird das schnell klar.
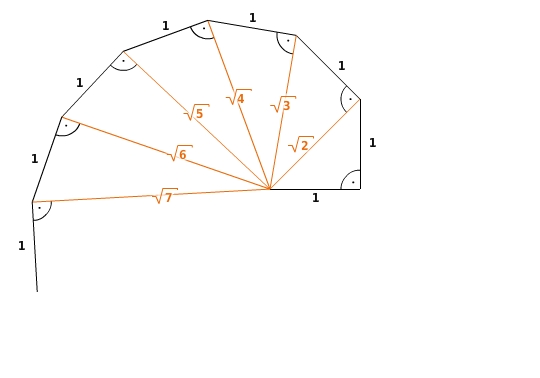

Diese Reihe kannst du weiter fortsetzen und auf diese Weise auch Strecken mit irrationalen Längen, wie z.B.
oder
, konstruieren.Die Figur die dabei entsteht wird „Wurzelschnecke“ genannt.Mit der Wurzelschnecke kannst du (theoretisch) die Quadratwurzel aus jeder natürlichen Zahl geometrisch als eine Streckenlänge darstellen.
Abstandsberechnungen im Koordinatensystem
Mit dem Satz des Pythagoras lässt sich eine Formel herleiten, mit der du den Abstand zweier Punkte aus deren Koordinaten berechnen kannst. Das Ergebnis liefert den exakten Wert und macht das Einzeichnen der Punkte im Koordinatensystem in vielen Fällen überflüssig.
Den Abstand d zwischen zwei Punkten
und
berechnest du mit der Abstandsformel
.
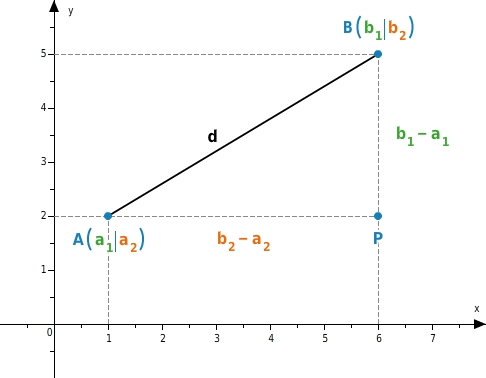 Der Abstand d zwischen den Punkten A und B ist gleich der Länge der Strecke
: Die Strecke
ist die Hypotenuse im rechtwinkligen Dreieck
. Die Kathete
hat die Länge
, die Kathete
hat die Länge
. Nach dem Satz des Pythagoras gilt:
Also :
Der Abstand d zwischen den Punkten A und B ist gleich der Länge der Strecke
: Die Strecke
ist die Hypotenuse im rechtwinkligen Dreieck
. Die Kathete
hat die Länge
, die Kathete
hat die Länge
. Nach dem Satz des Pythagoras gilt:
Also :
 Der Abstand d zwischen den Punkten A und B ist gleich der Länge der Strecke
: Die Strecke
ist die Hypotenuse im rechtwinkligen Dreieck
. Die Kathete
hat die Länge
, die Kathete
hat die Länge
. Nach dem Satz des Pythagoras gilt:
Also :
Der Abstand d zwischen den Punkten A und B ist gleich der Länge der Strecke
: Die Strecke
ist die Hypotenuse im rechtwinkligen Dreieck
. Die Kathete
hat die Länge
, die Kathete
hat die Länge
. Nach dem Satz des Pythagoras gilt:
Also :
Abstandsbestimmung im Koordinatensystem
Abstand d der Punkte
und
Du verwendest die Abstandsformel und setzt die Koordinaten in die Formel ein.


Eigenschaften eines Vierecks bestimmen
Ohne die Punkte
,
,
und
in ein Koordinatensystem einzutragen, kannst du entscheiden, dass das Viereck
ein Quadrat ist.
In einem Quadrat
1. sind alle vier Seiten gleich lang (Raute) und 2. alle Winkel sind rechte Winkel.
Seitenlängen:


Alle Strecken sind also gleich lang, die erste Bedingung ist erfüllt. Das Viereck ist eine Raute.
Rechter Winkel
Die Länge e der Diagonalen in der Raute
(mit der Seitenlänge a) ist der Abstand der Punkte A und C.Nach der Umkehrung des Satzes des Pythagoras hat das Dreieck ABC einen rechten Winkel im Punkt B wenn gilt:
 Also:
Also:
 Also:
Also:
In einer Raute mit einem rechten Winkel sind alle Winkel rechte Winkel. Die zweite Bedingung ist erfüllt.

