Umgang mit Flächeneinheiten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du von einer Flächeneinheit in eine andere umrechnest, wie du Flächeninhalte vergleichen und mit ihnen rechnen kannst.
Flächeneinheiten kennenlernen
Der Flächeninhalt einer ebenen Figur wird in den Einheiten Quadratkilometer (km?), Hektar (ha), Ar (a), Quadratmeter (m?), Quadratdezimeter (dm?), Quadratzentimeter (cm?) oder Quadratmillimeter (mm?) gemessen.
Das Flächenmaß „Quadratmeter“ basiert auf dem Längenmaß „Meter“. Ein Quadratmeter entspricht einer quadratischen Fläche von
:
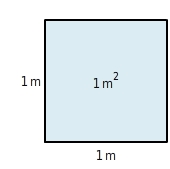 Die kleine 2 über dem m gibt an, dass die Maßeinheit „ins Quadrat genommen“, das heißt mit sich selbst multipliziert wurde.
Die kleine 2 über dem m gibt an, dass die Maßeinheit „ins Quadrat genommen“, das heißt mit sich selbst multipliziert wurde.

Die Einheiten Ar (
) und Hektar (
) sind heute vor allem noch in der Land- und Forstwirtschaft gebräuchlich, zum Beispiel zur Angabe der Größe einer Acker- oder einer Waldfläche.
Vergleichsgrößen zu den Flächeneinheiten
Für unterschiedlich große Flächen lässt sich eine jeweils angemessene Flächeneinheit finden. Die Fläche eines Klassenzimmers würde man beispielsweise nie in mm" sondern in m" angeben.
Um eine Vorstellung von den Größen der einzelnen Flächeneinheiten zu bekommen, kannst du dir passende Vergleichsgrößen merken:
: ein Stecknadelkopf  : ein Fingernagel
: ein Fingernagel  : eine Handfläche
: eine Handfläche  : ein Flügel einer Wandtafel
: ein Flügel einer Wandtafel  : eine Wohnung mit 4 Zimmern
: eine Wohnung mit 4 Zimmern  : ein Sportplatz mit Laufbahn
: ein Sportplatz mit Laufbahn  : ein großes Dorf
: ein großes Dorf 
 : ein Fingernagel
: ein Fingernagel  : eine Handfläche
: eine Handfläche  : ein Flügel einer Wandtafel
: ein Flügel einer Wandtafel  : eine Wohnung mit 4 Zimmern
: eine Wohnung mit 4 Zimmern  : ein Sportplatz mit Laufbahn
: ein Sportplatz mit Laufbahn  : ein großes Dorf
: ein großes Dorf 
Umrechnen von einer Flächeneinheit in eine andere
Bevor du Flächenangaben addieren oder subtrahieren kannst, musst du sicherstellen, dass sie die gleiche Einheit haben. Wenn nötig rechnest du eine Flächenangabe in eine andere Einheit um. Dafür gilt:
 Die Umrechnungszahl ist also immer
:
Die Umrechnungszahl ist also immer
:

 Die Umrechnungszahl ist also immer
:
Die Umrechnungszahl ist also immer
:

Wandle
in die nächstgrößere Einheit um.
Umwandeln
Die nächstgrößere Einheit ist a.
Du weißt, dass
=
sind.
Wandle
in die nächstkleinere Einheit um.
Umwandeln
Die nächstkleinere Einheit ist mm?.
Du weißt, dass
=
sind.
Unterschiedliche Schreibweisen von Flächenangaben
Eine Flächenangabe kannst du auf unterschiedliche Weise aufschreiben:



Aus der gemischten Schreibweise in die Kommaschreibweise umwandeln
Wandle um in Quadratmeter. Notiere mit Komma und vergiss die Einheit nicht!
Umwandeln
Nutze die Einheitentafel als Hilfe beim Umwandeln.
in der Einheitentafel:
 Die Fläche soll in m" angegeben werden. Das Komma steht also zwischen m" und dm?:
Endnullen nach dem Komma werden weggelassen.
Die Fläche soll in m" angegeben werden. Das Komma steht also zwischen m" und dm?:
Endnullen nach dem Komma werden weggelassen.
 Die Fläche soll in m" angegeben werden. Das Komma steht also zwischen m" und dm?:
Endnullen nach dem Komma werden weggelassen.
Die Fläche soll in m" angegeben werden. Das Komma steht also zwischen m" und dm?:
Endnullen nach dem Komma werden weggelassen.
Aus der Kommaschreibweise in die gemischte Schreibweise umwandeln
Wandle um in die gemischte Einheitenschreibweise.
Umwandeln
Nutze die Einheitentafel als Hilfe beim Umwandeln.
in der Einheitentafel:
 Die Fläche soll in cm" und mm" angegeben werden:
Da
=
sind, gehören zu einer Quadratmillimeter-Angabe immer zwei Ziffern (Zehner und Einer). In diesem Beispiel hat die Angabe in der Kommaschreibweise nur eine Nachkommastelle, deshalb schreibst du an die Einerstelle eine Null.
Die Fläche soll in cm" und mm" angegeben werden:
Da
=
sind, gehören zu einer Quadratmillimeter-Angabe immer zwei Ziffern (Zehner und Einer). In diesem Beispiel hat die Angabe in der Kommaschreibweise nur eine Nachkommastelle, deshalb schreibst du an die Einerstelle eine Null.
 Die Fläche soll in cm" und mm" angegeben werden:
Da
=
sind, gehören zu einer Quadratmillimeter-Angabe immer zwei Ziffern (Zehner und Einer). In diesem Beispiel hat die Angabe in der Kommaschreibweise nur eine Nachkommastelle, deshalb schreibst du an die Einerstelle eine Null.
Die Fläche soll in cm" und mm" angegeben werden:
Da
=
sind, gehören zu einer Quadratmillimeter-Angabe immer zwei Ziffern (Zehner und Einer). In diesem Beispiel hat die Angabe in der Kommaschreibweise nur eine Nachkommastelle, deshalb schreibst du an die Einerstelle eine Null.
Vergleichen von zwei Flächenangaben
Möchtest du wissen, welche Fläche die kleinere von Zweien ist, so vergleichst du die beiden Flächenangaben miteinander.
Man kann zwei Flächenangaben besonders einfach miteinander vergleichen, wenn sie in der gleichen Einheit gegeben sind.
Hier siehst du schnell, welche Flächenangabe kleiner ist:


Sind die Flächenangaben in unterschiedlichen Einheiten gegeben, wandelst du zunächst eine Angabe um.
Wenn du
in Quadratdezimeter umwandelst, erkennst du, dass die linke Flächenangabe größer ist:
>
Rechnen mit Flächeninhalten
Die Rechenoperationen Addition, Subtraktion, Multiplikation und Division lassen sich auch mit Flächeninhalten durchführen.
Du kannst zwei oder mehrere Flächeninhalte addieren:
... oder auch subtrahieren:
Du kannst einen Flächeninhalt vervielfachen, indem du ihn mit einer Zahl multiplizierst:
Du kannst einen Flächeninhalt durch eine Zahl, einen anderen Flächeninhalt oder eine Länge dividieren: Sind die Flächeninhalte in unterschiedlichen Einheiten gegeben, wandelst du erst eine der Angaben um und addierst oder subtrahierst dann:
Sind die Flächeninhalte in unterschiedlichen Einheiten gegeben, wandelst du erst eine der Angaben um und addierst oder subtrahierst dann:
 Sind die Flächeninhalte in unterschiedlichen Einheiten gegeben, wandelst du erst eine der Angaben um und addierst oder subtrahierst dann:
Sind die Flächeninhalte in unterschiedlichen Einheiten gegeben, wandelst du erst eine der Angaben um und addierst oder subtrahierst dann:
Addiere die Flächeninhalte.
Addieren
Wandle erst den Flächeninhalt mit der größeren Maßeinheit (
) in die kleinere Maßeinheit (cm?) um.

Subtrahiere die Flächeninhalte.
Subtrahieren
Wandle erst den Flächeninhalt mit der größeren Maßeinheit (
) in die kleinere Maßeinheit (dm?) um.


