Umfangsberechnung am Kreis
Online Mathe üben mit bettermarks
- Über 2.400 Übungen mit fast 200.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Hier erfährst du, welcher Zusammenhang zwischen dem Umfang und dem Durchmesser (oder Radius) besteht und wie du den Umfang von Kreisen berechnest.
Kreiszahl π
Bei jedem Kreis ist das Verhältnis von Umfang U zu Durchmesser d gleich. Dieses Verhältnis
(gesprochen: pi) ist eine Konstante und wird auch Kreiszahl genannt.
Die Gleichheit der Verhältnisse von Umfang zu Durchmesser von Kreisen kannst du dir mit Hilfe des ersten Strahlensatzes herleiten.Es gilt:
Die
ist eine irrationale Zahl also eine Dezimalzahl mit unendlich vielen Stellen nach dem Komma, die sich nicht periodisch wiederholen. Sie lässt sich nur näherungsweise angeben.
Die Kreiszahl
und ihre Berechnung fasziniert die Menschen schon seit über 3000 Jahren.
Heute übernehmen Computer die Stellenberechnung der Kreiszahl π. Der Japaner Y. Kanada hat 2002 mehr als 1,2 Billionen Stellen berechnen lassen. Der derzeitige Rekord (2010) sind 5 Billionen Stellen.Außerdem ist unter Denksportlern eine Art Wettkampf entbrannt, wer sich die meisten Stellen dieser Zahl merken kann. Das hat zu einprägsamen Sprüchen geführt, die die ersten Ziffern von π in verschlüsselter Form enthalten:Gib O Gott, O Vater Fähigkeit zu lernen!Die Anzahl der Buchstaben jedes Wortes gibt die einzelnen Ziffern von
an: 3,1415926…
Die Kreiszahl
und ihre Berechnung fasziniert die Menschen schon seit über 3000 Jahren.
Heute übernehmen Computer die Stellenberechnung der Kreiszahl π. Der Japaner Y. Kanada hat 2002 mehr als 1,2 Billionen Stellen berechnen lassen. Der derzeitige Rekord (2010) sind 5 Billionen Stellen.Außerdem ist unter Denksportlern eine Art Wettkampf entbrannt, wer sich die meisten Stellen dieser Zahl merken kann. Das hat zu einprägsamen Sprüchen geführt, die die ersten Ziffern von π in verschlüsselter Form enthalten:Gib O Gott, O Vater Fähigkeit zu lernen!Die Anzahl der Buchstaben jedes Wortes gibt die einzelnen Ziffern von
an: 3,1415926…
Kreisumfang
Aus dem Verhältnis des Kreisumfangs zum Kreisdurchmesser
ergibt sich die Formel für die Berechnung des Umfangs eines Kreises bei gegebenem Durchmesser d:
Hast du den Radius r des Kreises gegeben, verwendest du
, denn
Für den Umfang U eines Kreises mit dem Durchmesser d gilt:
Für den Umfang U eines Kreises mit dem Radius r gilt:
Berechne den Umfang U des Kreises mit dem Radius r =
. Runde das Ergebnis auf eine Stelle nach dem Komma.
Umfang berechnen
Den Umfang U berechnest du, indem du für den Radius in der Formel für den Kreisumfang den Wert 3,8 einsetzt: 
Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
.
Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
.
Der Kreis hat einen Umfang von etwa
.
Berechne den Radius r eines Kreises mit dem Umfang
.Gib das Ergebnis auf Zentimeter genau an.
Radius berechnen
Du stellst die Formel für die Berechnung des Umfangs U nach r um und setzt 35,706 für U ein: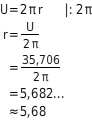
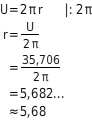Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
cm.
Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
cm.
Der Kreis hat hat einen Radius von etwa
.
Wachstum von Durchmesser und Umfang
Betrachtest du die Beziehung zwischen Umfang und Durchmesser (bzw. Radius) eines Kreises als proportionale Zuordnung, dann ist die Kreiszahl π der Proportionalitätsfaktor.Durch diese proportionale Zuordnung wird jedem Durchmesser eindeutig ein Umfang zugeordnet, es besteht also ein funktionaler Zusammenhang, der durch die lineare Funktion
beschrieben werden kann.Das heißt, vervielfacht sich der Durchmesser (bzw. Radius) mit einen Faktor, dann vervielfacht sich der Umfang mit demselben Faktor.
Kreisumfang in Sachzusammenhängen
Im Alltag hast du öfter mit kreisrunden Gegenständen zu tun, bei denen der Umfang von Interesse ist. Du kannst z.B. den Umfang eines Fahrradreifens berechnen und damit den zurückgelegten Weg bei einer bestimmten Anzahl von Radumdrehungen und daraus die Geschwindigkeit ermitteln.
Beim Longieren benutzt Lea eine Longierleine, die
lang ist. Welche Strecke hat das Pferd nach 25 Runden zurückgelegt" Gib das Ergebnis auf ganze Meter gerundet an.
Umfang berechnen
Zunächst berechnest du die Länge der Laufbahn, also den Umfang U des Longierkreises.Du setzt den Wert 8 für r in die Umfangsformel ein:
Das Pferd läuft 25 Runden (in m):
Das Pferd läuft 25 Runden (in m):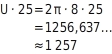
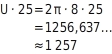
Die Laufstrecke des Pferdes beträgt etwa
.
Leon besitzt ein 24-Zoll-Fahrrad. Wenn Leon damit fährt, dreht sich der Reifen durchschnittlich 105 Mal pro Minute. Mit welcher Geschwindigkeit ist Leon unterwegs?Gib das Ergebnis auf Kilometer pro Stunde gerundet an.
Geschwindigkeit berechnen
Um die Geschwindigkeit v bestimmen zu können, benötigst du die Strecke s, die Leon in t Minuten zurücklegt, denn
.Die in einer Minute (
) zurückgelegte Strecke s ist das 105-fache des Reifenumfanges U, den du mit der Umfangsformel berechnen kannst.Die Angabe „24 Zoll“ ist das Maß für den Durchmesser des Reifens (1 Zoll =
).
Durchmesser des Reifens (in cm): 
Umfang des Reifens (in cm):
Da sich der Reifen pro Minute 105 Mal dreht, legt Leon in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
Eine Stunde hat 60 Minuten, also schafft es Leon in einer Stunde 60-mal so weit:
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an:
Umfang des Reifens (in cm):
Da sich der Reifen pro Minute 105 Mal dreht, legt Leon in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
Eine Stunde hat 60 Minuten, also schafft es Leon in einer Stunde 60-mal so weit:
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an:
Leon erreicht eine Geschwindigkeit von etwa
.