Übungen zum kleinen Einmaleins
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du mit dem kleinen Einmaleins und dem kleinen Einsdurcheins rechnen kannst.
Kleines Einmaleins
Das kleine Einmaleins solltest du auswendig können, damit du möglichst schnell rechnen kannst.
Das kleine Einmaleins benötigst du insbesondere für die schriftliche Multiplikation.
Mit null multiplizieren ergibt immer null!
Die farbig markierten Aufgaben sind die Kernaufgaben des kleinen Einmaleins. Sie sind leicht zu lernen und du kannst die schwierigeren Aufgaben daraus ableiten.
Die Multiplikationsaufgaben mit 1 und 10 stehen am Rand (orange markiert) und sind leicht zu lernen: bei der Multiplikation mit 1 bleibt die Zahl gleich und bei der Multiplikation mit 10 hängst du eine Null an(
,
, ... und
,
, ...).
Die Multiplikationsaufgaben mit 2 (grün) sind die Aufgaben, die du schnell durch verdoppeln herleiten kannst.
Die Multiplikationsaufgaben mit 5 (blau) kannst du leicht lernen, indem du die Aufgaben mit 10 halbierst(
).
Die Multiplikationsaufgaben mit gleichen Zahlen (blauer Rand) sind Quadratzahlen.
.
Multiplizieren mit null
und
Ergänzungsaufgaben
Rechne aus:
Multiplizieren
Du rechnest
und zerlegst das Ergebnis so, dass es insgesamt wieder 16 ergibt:
Rechne aus:
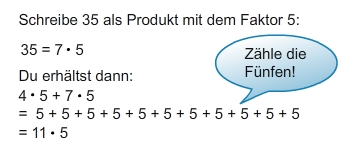
Multiplizieren
Kleines Einsdurcheins
Die Division ist die Umkehrung der Multiplikation. Wenn du eine Zahl (außer Null) mit einer Zahl multiplizierst und dann durch die gleiche Zahl wieder dividierst, dann erhältst du die Ausgangszahl.
Das kleine Einsdurcheins ist damit die Umkehrung des kleinen Einmaleins.
Wenn du null durch eine Zahl dividiert, erhältst du wieder null. Durch null kannst du jedoch nicht dividieren!
Du kannst nicht durch null dividieren!
Division als Umkehroperation
Multiplikation:
Umkehroperation (Division):
Division und die Null
ABER
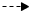geht nicht!
geht nicht!
Begründung:Die Umkehrung muss immer die Ausgangszahl liefern:
Egal welche Zahl man hier einsetzt, man kommt nicht zurück zu 5.
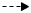
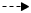Egal welche Zahl man hier einsetzt, man kommt nicht zurück zu 5.
