Symmetrie und Bewegungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, welche Kongruenzabbildungen es gibt, wie man sie erkennt und konstruiert. „Kongruenz“ stammt aus dem Lateinischen und bedeutet „übereinstimmung“. Es handelt sich also um Abbildungen, die Figuren in deckungsgleiche Figuren überführen.Der Begriff „Symmetrie“ kommt aus dem Griechischen (syn-= zusammen, metron = Maß) und bedeutet so viel wie „Gleichmaß“. Eine Figur ist symmetrisch, wenn sie durch eine Kongruenzabbildung (die identische ausgenommen) auf sich selbst abgebildet werden kann.
Achsenspiegelung
Eine Abbildung heißt Achsenspiegelung, wenn sie folgende Eigenschaften hat:Ein Punkt P und sein an der Achse gespiegelter Bildpunkt P‘ liegen auf einer zur Achse senkrechten Geraden. Beide haben denselben Abstand zur Achse.Punkte auf der Achse werden auf sich selbst abgebildet, sie sind Fixpunkte.Du kannst dir eine Achsenspiegelung so vorstellen:Sie ist eine Bewegung, bei der Figuren an einer Geraden „umgeklappt“ werden. Die Gerade nennt man Spiegelachse. Du kannst das Bild einer Figur auch erzeugen, wenn du einen Spiegel auf der Spiegelachse aufstellst und die gespiegelte Figur nachzeichnest.
Eine Spiegelung hat folgende Eigenschaften:Das Original einer Figur und ihr Spiegelbild sind deckungsgleich.
Strecken werden auf gleich lange Strecken abgebildet, Winkel auf gleichgroße Winkel, Geraden wieder auf Geraden, wobei auch die Parallelität von Geraden erhalten bleibt. Der Umlaufsinn einer Beschriftung der Figur ändert sich aber. Sind die Punkte der Originalfigur gegen den Uhrzeigersinn beschriftet, so sind die entsprechenden Bildpunkte im Uhrzeigersinn beschriftet. Man sagt, das Original und sein Spiegelbild sind entgegengesetzt orientiert.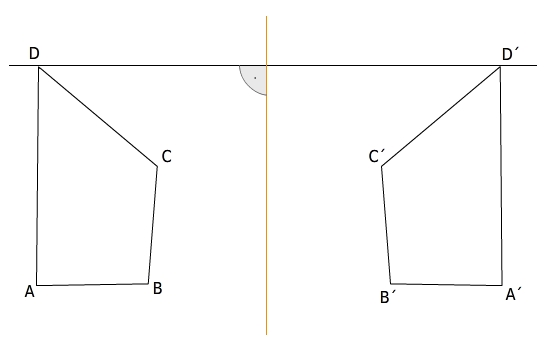

Achsenspiegelungen sind längen-, winkel- und geradentreu.
Bei einer Achsenspiegelung wird die Orientierung umgedreht.
Eine Figur heißt achsensymmetrisch, wenn sie mindestens eine Spiegelachse besitzt, also eine Hälfte der Figur das Spiegelbild der anderen Hälfte ist. Es gibt Figuren mit mehreren Symmetrieachsen. Der Kreis hat sogar unendlich viele Symmetrieachsen.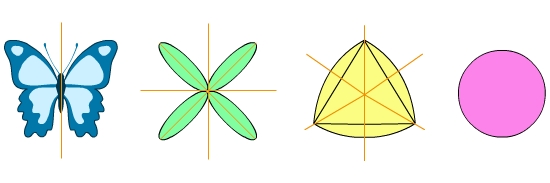

Ein Dreieck an einer Geraden spiegeln
Spiegele das Dreieck an der vorgegebenen Achse.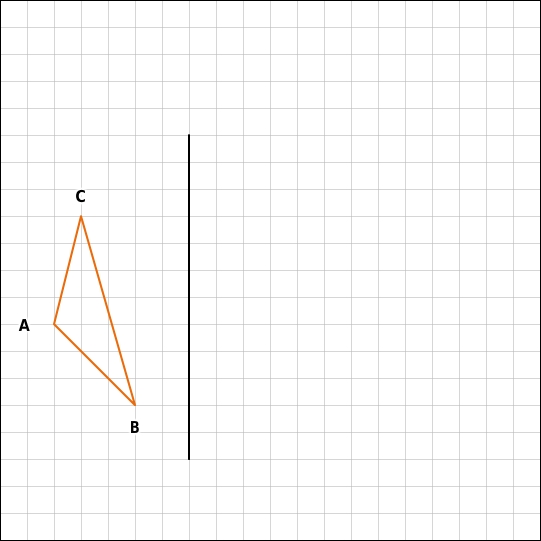
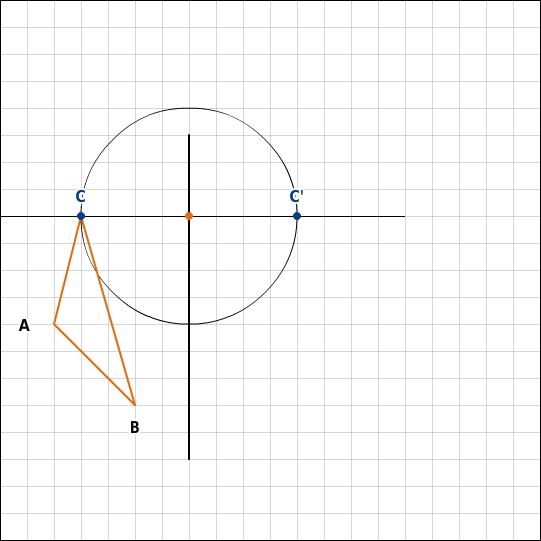


Punkt C spiegeln
- Du spiegelst einen Punkt C des Dreiecks, indem du eine Gerade konstruierst, die senkrecht zur Spiegelachse durch den Punkt C verläuft. - Danach kannst du mit dem Zirkel den Bildpunkt C' markieren, der zur Achse denselben Abstand hat wie C.

Punkte verbinden
- Die Punkte A und B spiegelst du genauso wie den Punkt C und verbindest anschließend die Bildpunkte A‘, B‘ und C‘.

Drehung
Eine Abbildung heißt Drehung um Z um den Winkel
, wenn sie die folgenden Eigenschaften hat:Der Bildpunkt von Z ist Z, das heißt Z ist ein Fixpunkt.Für jeden anderen Punkt P gilt: P und der Bildpunkt P' haben von Z den gleichen Abstand und schließen mit Z den Winkel
ein.Den Fixpunkt Z nennt man Drehzentrum, den Winkel
Drehwinkel.Du kannst dir eine Drehung so vorstellen:Eine Drehung ist eine Bewegung, bei der ein Punkt Z festbleibt. Alle anderen Punkte bewegen sich auf Kreisen um diesen Punkt um einen festen Winkel.
Eine Drehung hat folgende Eigenschaften:Das Original einer Figur und ihr Spiegelbild sind deckungsgleich.Strecken werden auf gleich lange Strecken abgebildet, Winkel auf gleichgroße Winkel, Geraden wieder auf Geraden, wobei auch die Parallelität von Geraden erhalten bleibt. Der Umlaufsinn einer Beschriftung der Figur ändert sich nicht. Sind die Punkte der Originalfigur gegen den Uhrzeigersinn beschriftet, so sind die entsprechenden Bildpunkte ebenfalls gegen den Uhrzeigersinn beschriftet. Man sagt, das Original und sein Spiegelbild sind gleich orientiert.Eine Drehung kann auch durch zwei hintereinander ausgeführte Achsenspiegelungen erzeugt werden. Dazu wählst du zwei Halbgeraden, die den Drehwinkel einschließen. Als erste Spiegelachse wählst du einen der Schenkel, als zweite Spiegelachse die Winkelhalbierende des eingeschlossenen Drehwinkels.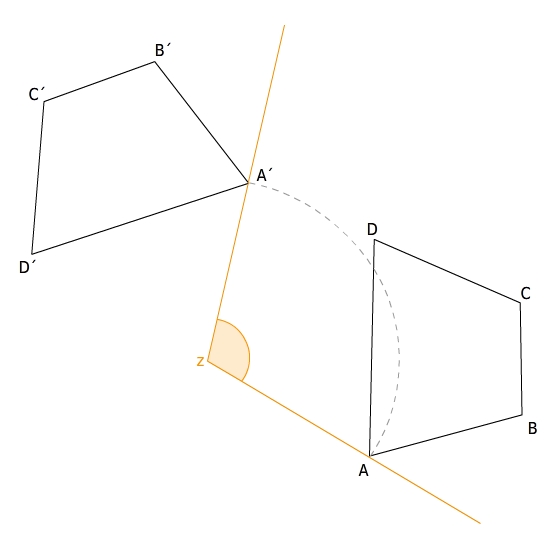 Eine Figur heißt drehsymmetrisch, wenn sie ein Drehzentrum hat, es also einen Punkt gibt, um den man die Figur so drehen kann, dass sie mit sich selbst zur Deckung kommt. Der Drehwinkel muss dabei kleiner als
und größer als
sein.
Eine Figur heißt drehsymmetrisch, wenn sie ein Drehzentrum hat, es also einen Punkt gibt, um den man die Figur so drehen kann, dass sie mit sich selbst zur Deckung kommt. Der Drehwinkel muss dabei kleiner als
und größer als
sein.
 Eine Figur heißt drehsymmetrisch, wenn sie ein Drehzentrum hat, es also einen Punkt gibt, um den man die Figur so drehen kann, dass sie mit sich selbst zur Deckung kommt. Der Drehwinkel muss dabei kleiner als
und größer als
sein.
Eine Figur heißt drehsymmetrisch, wenn sie ein Drehzentrum hat, es also einen Punkt gibt, um den man die Figur so drehen kann, dass sie mit sich selbst zur Deckung kommt. Der Drehwinkel muss dabei kleiner als
und größer als
sein.
Diese Figur ist drehsymmetrisch. Sie kann um
,
und
um ihren Mittelpunkt gedreht werden. Dabei werden sie immer auf sich selbst abgebildet.

Diese Figur ist ebenfalls drehsymmetrisch. Sie kann um
und
um ihren Mittelpunkt gedreht werden.
Drehungen sind längen-, winkel- und geradentreu und erhalten die Orientierung
Drehe das Dreieck um
.

Figur drehen
- Du drehst das Dreieck, indem du seine drei Eckpunkte drehst und dann die Punkte zum Bilddreieck verbindest. - Um den Bildpunkt von A zu bestimmen, verbindest du zunächst A mit Z. Dann trägst du den Drehwinkel an der Geraden in Z ab. Dann markierst du mit dem Zirkel den Punkt A‘ auf dem neuen Schenkel, der denselben Abstand wie A zu Z hat.- Mit den anderen Punkten verfährst du genauso und verbindest anschließend die Bildpunkte.

Punktspiegelung
Eine Abbildung heißt Punktspiegelung am Punkt Z, wenn sie die folgenden Eigenschaften hat:Der Bildpunkt von Z ist Z.Für jeden anderen Punkt P gilt:P und der Bildpunkt P' haben von Z den gleichen Abstand, und Z ist der Mittelpunkt der Strecke
. Jede Punktspiegelung ist eine Drehung um Z mit dem Drehwinkel
.Du kannst dir die Punktspiegelung also als Drehung um Z mit dem Drehwinkel
vorstellen.Die Punktspiegelung hat folgende Eigenschaften:Das Original einer Figur und ihr Spiegelbild sind deckungsgleich.Strecken werden auf gleich lange Strecken abgebildet, Winkel auf gleichgroße Winkel, Geraden wieder auf Geraden, wobei auch die Parallelität von Geraden erhalten bleibt. Der Umlaufsinn einer Beschriftung der Figur ändert sich nicht. Sind die Punkte der Originalfigur gegen den Uhrzeigersinn beschriftet, so sind die entsprechenden Bildpunkte ebenfalls gegen den Uhrzeigersinn beschriftet. Man sagt, das Original und sein Spiegelbild sind gleich orientiert.Eine Punktspiegelung kann auch durch zwei hintereinander ausgeführte Achsenspiegelungen erzeugt werden. Dabei müssen die beiden Spiegelachsen durch Z gehen und senkrecht aufeinander stehen.
Eine Figur heißt punktsymmetrisch, wenn sie einen Symmetriepunkt hat, es also einen Punkt gibt, um den man die Figur um
drehen kann, ohne sie dabei zu verändern.

Punktspiegelungen sind längen-, winkel- und geradentreu und erhalten die Orientierung.
Eine Punktspiegelung ist eine Drehung um
.
Ein Dreieck an einem Punkt spiegeln
Spiegele das Dreieck am vorgegebenen Punkt Z.

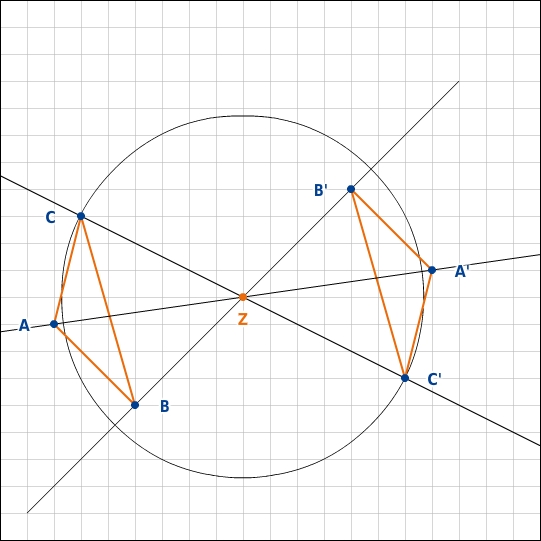

Punkt punktspiegeln
- Du spiegelst das Dreieck, indem du alle drei Punkte an Z spiegelst und anschließend miteinander verbindest.- Du spiegelst den Eckpunkt C an Z, indem du eine Hilfsgerade durch C und Z legst.- Anschließend kannst du von Z aus den Bildpunkt C' markieren, der zu Z denselben Abstand wie C hat.

Punkte verbinden
Mit den anderen Punkten verfährst du genauso und verbindest anschließend die Bildpunkte A', B' und C'.

Verschiebung
Eine Abbildung heißt Verschiebung (auch Parallelverschiebung), wenn sie folgende Eigenschaften hat: Jeder Punkt einer Figur wird um die gleiche Länge und in die gleiche Richtung verschoben. Die Verschiebung eines Punktes P auf seinen Bildpunkt P" wird durch einen Verschiebungspfeil gekennzeichnet.Eine Figur und die verschobene Figur sind deckungsgleich, denn jede Verschiebung ist eine Kongruenzabbildung: Strecken werden auf gleich lange Strecken abgebildet, Winkel auf gleichgroße Winkel, Geraden wieder auf Geraden, wobei auch die Parallelität von Geraden erhalten bleibt. Der Umlaufsinn der Beschriftung ändert sich nicht. Die Originalfigur und die verschobene Figur sind gleich orientiert.Eine Parallelverschiebung kann auch durch zwei hintereinander ausgeführte Achsenspiegelungen bewirkt werden. Du zeichnest eine Strecke, deren Länge und Richtung durch den Verschiebungspfeil gegeben sind. Als erste Spiegelachse wählst du die Gerade, die senkrecht auf einem der Endpunkte dieser Strecke steht, als zweite Spiegelachse die Mittelsenkrechte der Strecke.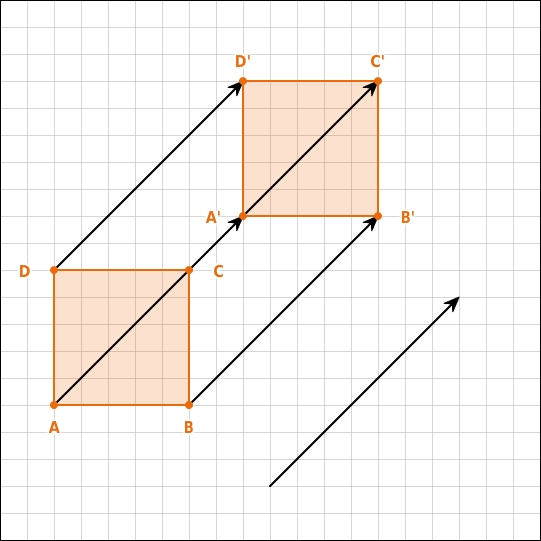

Verschiebungen sind längen-, winkel-, geradentreu und erhalten die Orientierung.
Verschiebungen können auch durch zwei hintereinander ausgeführte parallele Achsenspiegelungen dargestellt werden. Der Abstand der beiden Achsen ist dabei halb so groß wie die Länge der Verschiebung.
Ein Dreieck verschieben
Verschiebe das Dreieck entlang des vorgegebenen Verschiebungspfeiles.


Figur verschieben
- Du verschiebst ein Dreieck, indem du alle drei Punkte um die Länge und Richtung des Verschiebungspfeiles verschiebst.- Du verschiebst einen Punkt, indem du eine Gerade zeichnest, die parallel zum Verschiebungspfeil und durch den Punkt verläuft. - Mit dem Zirkel kannst du dann die exakte Länge des Pfeiles vom Punkt aus abtragen und erhältst den zugehörigen Bildpunkt.- Mit den anderen Eckpunkten verfährst du genauso und verbindest anschließend die zugehörigen Bildpunkte.


