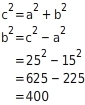Satz des Pythagoras
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenDer Satz des Pythagoras
Fast jeder hat den Satz schon einmal gehört: . Du kannst die Aussage des Satzes nachvollziehen, wenn du über den Seiten eines rechtwinkligen Dreiecks jeweils ein Quadrat zeichnest. Dann erhältst du diese Figur: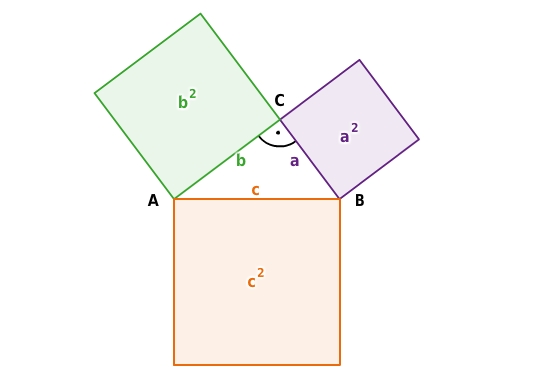 
In einem rechtwinkligen Dreieck mit dem rechten Winkel im Punkt sind und die Längen der und die der . Es ist der Flächeninhalt des Quadrats über der Kathete der Länge , der Flächeninhalt des Quadrats über der Kathete der Länge und der Flächeninhalt des Quadrats über der Hypotenuse.
Satz des PythagorasIn einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der beiden Quadrate über den Katheten der Längen und gleich dem Flächeninhalt des Quadrats über der Hypotenuse der Länge .Als Formel:
Flächeninhalt eines Kathetenquadrats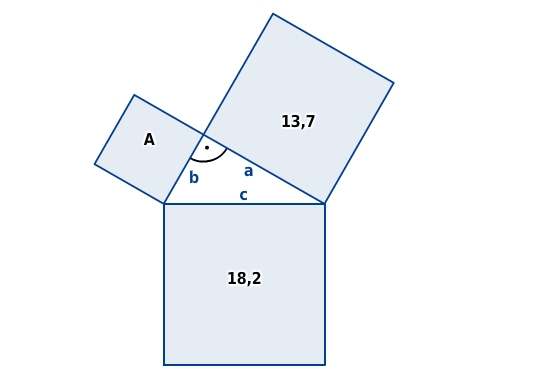 
Nach dem Satz des Pythagoras gilt: Du stellst nach um und setzt die Werte ein.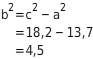
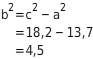
Der Satz des Pythagoras gilt aber auch in jedem anders bezeichneten rechtwinkligen Dreieck.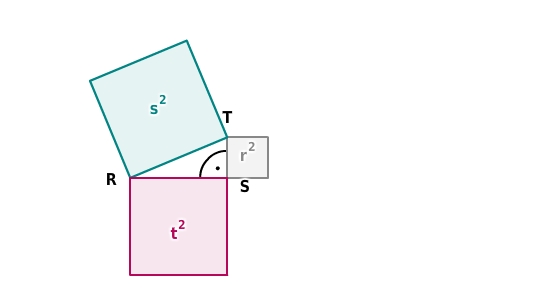
Im Dreieck liegt der rechte Winkel am Punkt .Hier ist die Länge der Hypotenuse und die Längen der Katheten sind bzw. .
Im Dreieck liegt der rechte Winkel am Punkt .Hier ist die Länge der Hypotenuse und die Längen der Katheten sind bzw. .Seitenlängen im rechtwinkligen Dreieck berechnen
Mit dem Satz des Pythagoras lassen sich nicht nur Flächeninhalte berechnen, sondern auch die Seitenlängen eines rechtwinkligen Dreiecks.
Länge der Hypotenuse (in )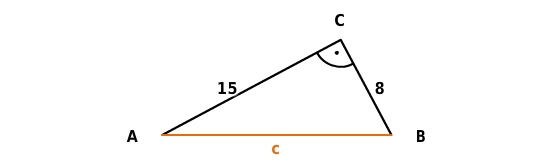
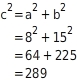Also:
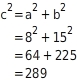
Länge einer Kathete (in )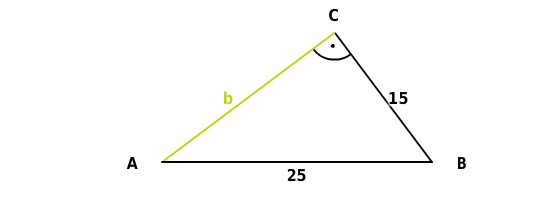
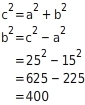Also:
