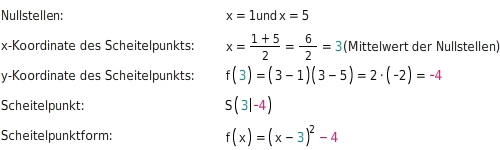Rechnerische Bestimmung der Scheitelpunktform
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenVon der allgemeinen Form zur Scheitelpunktform
Mit der quadratischen Ergänzung bringst du den Funktionsterm f(x)=ax2+bx+c in die Scheitelpunktform f(x)=a(x-d)2+e .
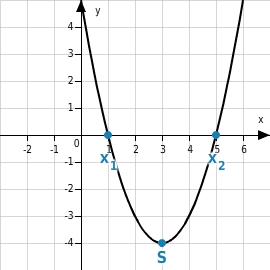
Von der faktorisierten Form zur Scheitelpunktform
Mit Hilfe der Nullstellen der Funktion bringst du die faktorisierte Form f(x)=a(x-x1)(x-x2) in die Scheitelpunktform f(x)=a(x-d)2+e Dazu ermittelst du die Koordinaten des Scheitelpunkts der zugehörigen Parabel : Die x-Koordinate ist der Mittelwert der beiden Nullstellen, die y-Koordinate der Funktionswert an dieser Stelle. 
