Rechnen mit Potenzen mit rationalem Exponenten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit Potenzen mit rationalen Exponenten und mit Wurzeln mit beliebigen ganzzahligen Wurzelexponenten rechnen kannst.
Die n-te Wurzel
Potenzieren und Radizieren sind Umkehroperationen.
Zum Quadrieren (Potenzieren mit 2) gehört die Quadratwurzel:
und
Der Wurzelexponent 2 wird meist weggelassen.
Zum Potenzieren mit 3 gehört die Kubikwurzel (dritte Wurzel).
und
Genauso gibt es auch die vierte, fünfte, sechste usw. Wurzel.
und
Allgemein gilt:
Für alle Zahlen
0 ist
diejenige nichtnegative Zahl
, für die gilt:
. Dabei ist
eine natürliche Zahl..
Sprich:
-te Wurzel aus
, also
Mit Hilfe der
-ten Wurzel kannst du Gleichungen mit Potenzen lösen.
Die Lösungsmenge für
ist L = {
} = {5}, denn
.
Die Lösungsmenge für
ist L = {
;
}= {
;
}, denn
und
.
Die Lösungsmenge für
ist L = {
}= {
}, denn
.
Es ist zwar
, aber
.gibt es nicht, da Wurzeln aus negativen Zahlen nicht definiert werden.
Potenzen mit rationalen Exponenten
Die
-ten Wurzeln lassen sich auch als Potenz schreiben.
Für
0 und
∈ ℕ gilt:
Das gilt auch für Wurzeln, deren Radikand selbst eine Potenz ist.
Für
und
,
∈ ℕ gilt:
und
Diese Potenzen heißen Potenzen mit rationalen Exponenten. Für positive Exponenten darf auch
sein:
.
Du kannst also jede Wurzel als Potenz mit rationalem Exponenten und jede Potenz mit rationalem Exponenten als Wurzel schreiben.
Je nachdem, wie du mit dem Wurzelterm weiter rechnen möchtest, kannst du die Potenz auch ausrechnen.
Bei der Berechnung einer Potenz mit rationalem Exponenten ist es egal, ob du erst die Wurzel ziehst und dann potenzierst oder umgekehrt.
ist die 3. Wurzel aus der 2. Potenz von 8.oder
ist die 2. Potenz der 3. Wurzel aus 8.
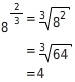 oder
oder

In manchen Fällen bietet sich eine bestimmte Reihenfolge aber an.

Da 25 eine Quadratzahl ist, ziehst du erst die Wurzel und potenzierst dann mit 3.
Sind Wurzelexponent und Exponent des Radikanden nicht teilerfremd, kannst du den Radikanden als Potenz schreiben, bei der der Exponent gekürzt werden kann. Dadurch kann sich aber der Definitionsbereich ändern.

Der Term
ist nur für
0 definiert,der Term
dagegen für alle
∈ ℝ.Die Gleichheit bzw. äquivalenz beider Terme ist also nur für alle
0 erfüllt.
Potenzgesetze
Für Potenzen mit rationalen Exponenten gelten die Potenzgesetze.
Potenzen mit gleicher BasisFür rationale Zahlen
und
und positive reelle Zahlen
gilt:
und
Für positive Exponenten darf beim Multiplizieren auch
sein:
. Die Division durch 0 ist jedoch nicht möglich.
Fasse
zusammen und schreibe als Wurzel.


Du wendest das Potenzgesetz für Potenzen mit gleicher Basis an.


Fasse
zusammen und schreibe als Wurzel.
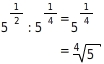
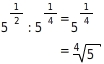
Du wendest das Potenzgesetz für Potenzen mit gleicher Basis an.
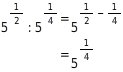
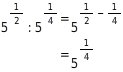
Potenzen mit gleichem ExponentenFür rationale Zahlen
und positive reelle Zahlen
und
gilt:
und
Fasse
zusammen und schreibe als Wurzel.


Du wendest das Potenzgesetz für Potenzen mit gleichen Exponenten an.
Fasse
zusammen und schreibe als Wurzel.
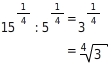
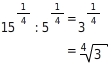
Du wendest das Potenzgesetz für Potenzen mit gleichen Exponenten an.
Potenzen von PotenzenFür rationale Zahlen
und
und positive reelle Zahlen
gilt:
Fasse
zusammen und schreibe als Wurzel.
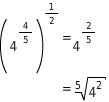
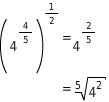
Du wendest das Potenzgesetz für Potenzen von Potenzen an und kürzt im Exponenten.
So, wie du eine Potenz potenzieren kannst, kannst du auch aus einer Wurzel eine Wurzel ziehen.
Schreibe
als eine Wurzel.
Du schreibst beide Wurzeln als Potenzen und wendest das Potenzgesetz für Potenzen von Potenzen an: