Rechengesetze für Wurzeln
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit Wurzeln rechnest und welche Regeln du dabei beachten musst.Wurzeln, die irrationale Zahlen sind, können nur als Näherungswert berechnet werden. Deshalb ist das Ziel beim Umformen von Wurzeltermen, als Radikanden die kleinstmögliche natürliche Zahl zu erhalten und möglichst viele Wurzeln ganz zu entfernen.
Multiplizieren und dividieren
Mit Wurzeln kannst du rechnen wie mit anderen Zahlen auch.
Multiplikation einer Zahl mit einer Wurzel
Wenn eine ganze Zahl und eine Wurzel miteinander multipliziert werden, wird üblicherweise das Multiplikationszeichen nicht geschrieben.
Multiplikation und Division zweier Wurzeln
Die Wurzel eines Produkts kannst du in das Produkt zweier Wurzeln umwandeln, ebenso kannst du die Wurzel eines Quotienten in den Quotienten zweier Wurzeln umwandeln.
Also:
Multiplikationsregel:
für
,
0
Divisionsregel:
für
0 und
> 0
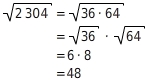
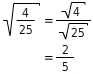
Beim Multiplizieren zweier Binome mit Wurzeln gehst du genauso vor wie bei Binomen ohne Wurzel, du wendest das Distributivgesetz an.
Vereinfache: 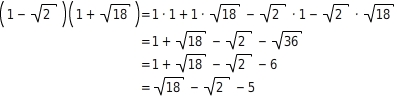
Ausmultiplizieren und Zusammenfassen
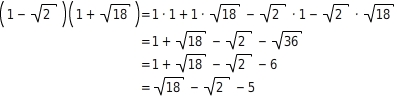
Addieren und subtrahieren
Für das Addieren und Subtrahieren von Wurzeln gibt es keine Vereinfachungsregel. Beachte, dass stets
≠
für
,
> 0
und
≠
für
>
> 0 gilt.
Vergleiche
und
.
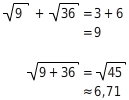
Du kannst auf Summen und Differenzen von Termen mit Wurzeln auch das Distributivgesetz anwenden und Wurzeln ausklammern.
und
für
,
,
∈ ℝ und
> 0.
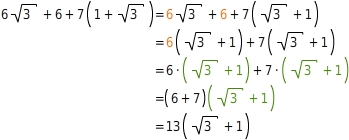
Teilweise Wurzelziehen
Mit Hilfe der Rechengesetze kannst du teilweise Wurzeln ziehen. Das bedeutet, du zerlegst den Radikanden in ein Produkt aus Quadratzahlen und Zahlen, die keine Quadratzahlen sind. Mit der Multiplikationsregel zerlegst du die Wurzel des Produktes in ein Produkt aus Wurzeln. Die Wurzel der Quadratzahlen kannst du dann berechnen.
für
,
0
Du faktorisierst den Radikanden
4 ist eine Quadratzahl, also:
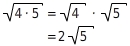
Ziehe teilweise die Wurzel aus 756.
Radikand faktorisieren
Um die größtmögliche Quadratzahl zu finden, zerlegst du 756 in Primfaktoren:
Also:
Du fasst jeweils eine gerade Anzahl gleicher Faktoren zu einer Potenz mit geradigem Exponenten zusammen:
Die Potenzen mit geradzahligen Exponenten kannst du zu einer Quadratzahl zusammenfassen:
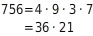
Teilweise Wurzel ziehen
Du ziehst nun teilweise die Wurzel:
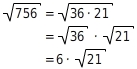
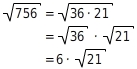
Umgekehrt kannst du auch eine Zahl der Form
mit
,
0 in eine Wurzel
umwandeln. Dafür schreibst du
als Wurzel ihres Quadrats und bringst dieses zusammen mit
unter die Wurzel.
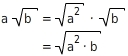
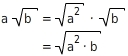
Brüche mit Wurzeltermen im Nenner
Brüche, in deren Nenner eine Wurzel steht, kannst du durch geschicktes Erweitern des Bruches so umformen, dass der Nenner keine Wurzel mehr enthält.
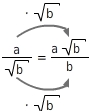
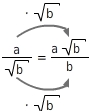
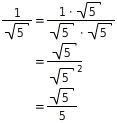
Forme so um, dass der Nenner keine Wurzel mehr enthält.
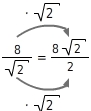
Erweitern

Kürzen
8 und 2 kannst du kürzen.

