Rationalmachen des Nenners
Online Mathe üben mit bettermarks
- Über 2.000 Übungen mit über 100.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Hier erfährst du, wie du einen Bruchterm so umformst, dass der Nenner keine Wurzelterme mehr enthält.
Diese Umformungen heißen Rationalmachen des Nenners, wobei zwei Fälle unterschieden werden:
Es kann vorkommen, dass der umgeformte Term einen anderen Definitionsbereich hat als der ursprüngliche Term. Die Umformungen sind immer nur für den kleineren Definitionsbereich äquivalenzumformungen.
Es kann vorkommen, dass der umgeformte Term einen anderen Definitionsbereich hat als der ursprüngliche Term. Die Umformungen sind immer nur für den kleineren Definitionsbereich äquivalenzumformungen.
Bruchterme mit einfachem Wurzelterm im Nenner
Sind der Zähler und der Radikand der Wurzel im Nenner nicht teilerfremd, kannst du mit der Wurzel des größten gemeinsamen Teilers kürzen.
Für jede nicht negative reelle Zahl
gilt:
.Du kannst also den Zähler in ein Produkt umwandeln und dann den Bruch kürzen:
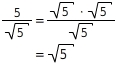
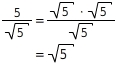
5 ist ein Teiler von 10.Du zerlegst den Zähler und kürzt:
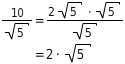
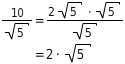
Steht im Nenner nur eine Wurzel und ist Kürzen nicht möglich, dann erweiterst du den Bruch mit genau dieser Wurzel.Die Wurzel wird dabei mit sich selbst multipliziert (quadriert).
Du erweiterst den Bruch mit
und fasst jeweils den Zähler und den Nenner so weit wie möglich zusammen:
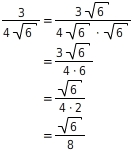
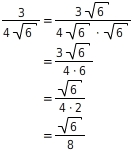
Du erweiterst den Bruch mit
, wendest die Multiplikationsregel an und fasst jeweils den Zähler und den Nenner so weit wie möglich zusammen:
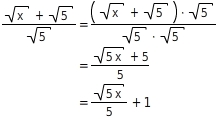
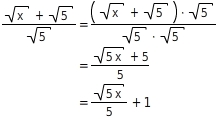
Du erweiterst den Bruch mit
, wendest die Multiplikationsregel an und fasst jeweils den Zähler und den Nenner so weit wie möglich zusammen:
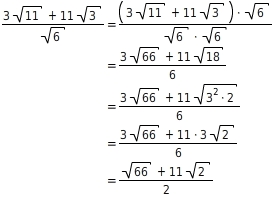
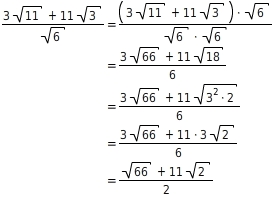
Manchmal bietet es sich an, vor dem Erweitern mit „einem Teil“ der Wurzel im Nenner zu kürzen.
10 und 15 haben den gemeinsamen Teiler 5.Du zerlegst den Zähler und den Nenner und kürzt:
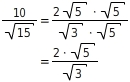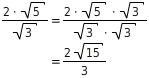
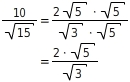Jetzt kannst du durch Erweitern mit
den Nenner rational machen:
Jetzt kannst du durch Erweitern mit
den Nenner rational machen:
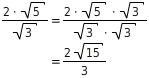
Oft kannst du vor dem Erweitern den Wurzelterm im Nenner noch vereinfachen, indem du teilweise die Wurzel ziehst.
für
0
Du ziehst im Nenner teilweise die Wurzel, denn
und
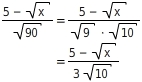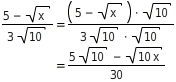
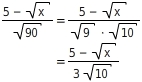Jetzt kannst du durch Erweitern mit
den Nenner rational machen:
Jetzt kannst du durch Erweitern mit
den Nenner rational machen:
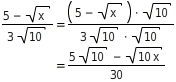
Bei anderen Termen kann es hilfreich sein, eine Summe oder Differenz aus zwei Brüchen zu einem Bruch zusammenzufassen.
für
0
Du bildest zunächst den Hauptnenner und erweiterst dann mit dem Wurzelterm des Nenners:Der Hauptnenner ist
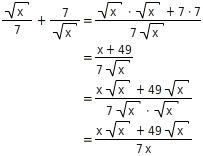
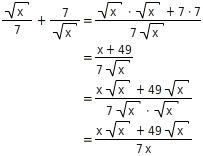
Bruchterme mit Binom im Nenner
Steht im Nenner eine Summe oder Differenz, die Wurzeln enthält, erweiterst du den Bruch mit der entsprechenden Differenz oder Summe. Durch Anwenden der dritten binomischen Formel
entfallen die Wurzeln im Nenner.
Im Nenner steht eine Differenz:
Erweiterst du den Bruch mit
, kannst du die dritte binomische Formel anwenden, denn
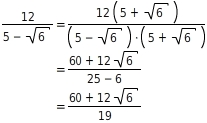
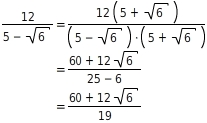
Du erweiterst mit
und erhältst durch Kürzen sogar einen Term ohne Bruch.
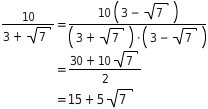
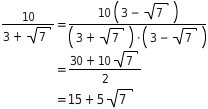
änderung des Definitionsbereichs
Bei Bruchtermen mit Variablen kann sich durch Beseitigen der Wurzel im Nenner der Definitionsbereich ändern.Der Term vor der Umformung ist dann nicht immer für alle Zahlen seines Definitionsbereichs äquivalent zum umgeformten Term.Um zu bestimmen, für welche Werte beide Terme äquivalent sind, ermittelst du die Definitionsbereiche beider Terme und bestimmst ihren gemeinsamen Definitionsbereich.
für
∈ ℝ mit
0 und
≠ 1
Beim linken Term überprüfst du, für welche Werte von
die Wurzeln definiert sind und wählst als Voraussetzung
0.Damit ist auch die Bedingung, dass der Nenner nicht null werden darf, erfüllt.Nach der Umformung ist der Nenner eine Differenz.Der Definitionsbereich ist also kleiner geworden, weil
von 1 verschieden sein muss, denn für
ist
.