Nullstellen- und Schnittpunktberechnungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenNullstellen einer Parabel
Die Nullstellen einer Funktion f sind die x-Werte, für die die Funktion den Wert null annimmt. An einer Nullstelle
gilt also
.
An einer Nullstelle schneidet bzw. berührt der Graph von f die x-Achse. Die Anzahl der Nullstellen einer quadratischen Funktion hängt von der Lage der zugehörigen Parabel ab.
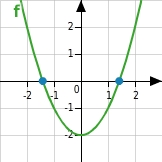
Funktion f mit
Die zugehörige Parabel ist nach oben geöffnet und ihr Scheitelpunkt liegt unterhalb der x-Achse.
Sie schneidet die x-Achse zweimal und somit hat die Funktion f zwei Nullstellen.

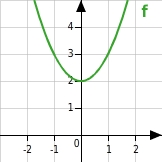
Funktion f mit
Die zugehörige Parabel ist nach oben geöffnet und ihr Scheitelpunkt liegt oberhalb der x-Achse.
Sie schneidet die x-Achse in keinem Punkt und somit hat die Funktion f keine Nullstelle.

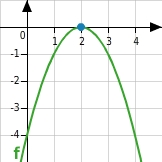
Funktion f mit
Die zugehörige Parabel ist nach unten geöffnet und ihr Scheitelpunkt liegt auf der x-Achse.
Sie berührt die x-Achse in einem Punkt und somit hat die Funktion f genau eine Nullstelle.

Nullstellen berechnen
Um die Nullstellen einer Funktion zu berechnen, setzt du den Funktionsterm gleich null und löst die Gleichung.
Funktion f mit
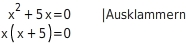
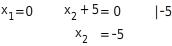
Funktion f mit
Lösen mit pq-Formel:
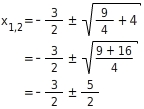 und
und
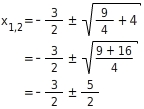 und
und
Funktion f mit
Lösen mit abc-Formel:
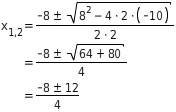 und
und
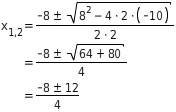 und
und
Anzahl der Nullstellen anhand der Diskriminante bestimmen
Die Anzahl der Nullstellen einer quadratischen Funktion f entspricht der Anzahl der Lösungen der quadratischen Gleichung
. Daher kannst du die Anzahl der Nullstellen anhand der Diskriminante der quadratischen Gleichung bestimmen.
.
Die Gleichung hat zwei Lösungen.
Die Funktion f mit
hat also zwei Nullstellen.
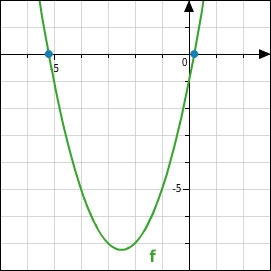

.
Die Gleichung hat keine Lösung.
Die Funktion f mit
hat also keine Nullstellen.
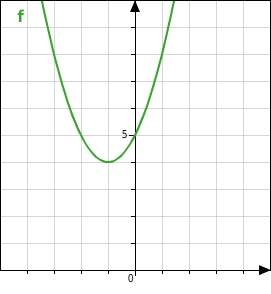

Schnittpunkte zweier Graphen
Um die Schnittpunkte der Graphen zweier Funktionen f und g zu bestimmen, setzt du die Funktionsterme gleich und löst die entstandene Gleichung nach x auf.
Die Schnittpunkte haben die Koordinaten
.
Funktionen f und g mit
und
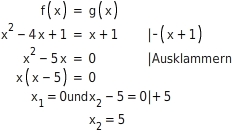 Einsetzen der Werte in eine der beiden Funktionen
und
ergibt die Schnittpunkte
und
.
Einsetzen der Werte in eine der beiden Funktionen
und
ergibt die Schnittpunkte
und
.
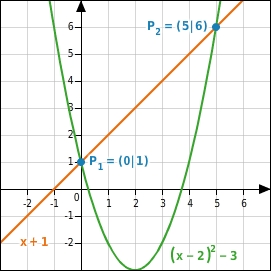
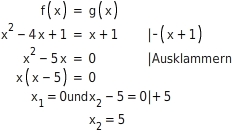 Einsetzen der Werte in eine der beiden Funktionen
und
ergibt die Schnittpunkte
und
.
Einsetzen der Werte in eine der beiden Funktionen
und
ergibt die Schnittpunkte
und
.

Anzahl der Schnittpunkte zweier Parabeln
Oft kannst du schon anhand der Lage zweier Parabeln im Koordinatensystem entscheiden, ob sie sich schneiden.
Am einfachsten kannst du die Lage einer Parabel im Koordinatensystem erkennen, wenn die Parabelgleichung in Scheitelpunktform gegeben ist.
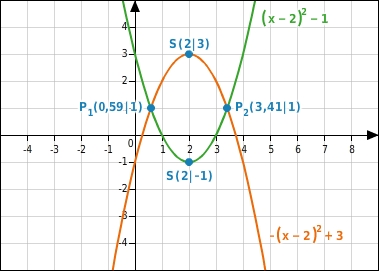
Parabel 1:
Die Parabel ist nach oben geöffnet.
Ihr Scheitelpunkt
liegt im ersten Quadranten.
Parabel 2:
Die Parabel ist nach unten geöffnet.
Ihr Scheitelpunkt
liegt im vierten Quadranten.
Die beiden Parabeln schneiden sich nicht.
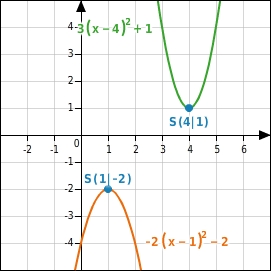

Parabel 1:
Die Parabel ist nach oben geöffnet.
Ihr Scheitelpunkt
liegt im vierten Quadranten.
Parabel 2:
Die Parabel ist nach unten geöffnet.
Ihr Scheitelpunkt
liegt im ersten Quadranten.
Die beiden Parabeln schneiden sich zweimal.