Newton-Verfahren

Das Newtonsche Näherungsverfahren erlaubt es, rekursiv eine Nullstelle beliebig genau zu berechnen, falls die Funktionsgleichung differenzierbar ist. Ist eine Funktion mindestens zweimal differenzierbar, für  in der Nähe einer Nullstelle, so schneidet die Tangente in die x-Achse an der Stelle und der neue Wert ist in viele Fällen eine bessere Näherung an die Nullstelle.

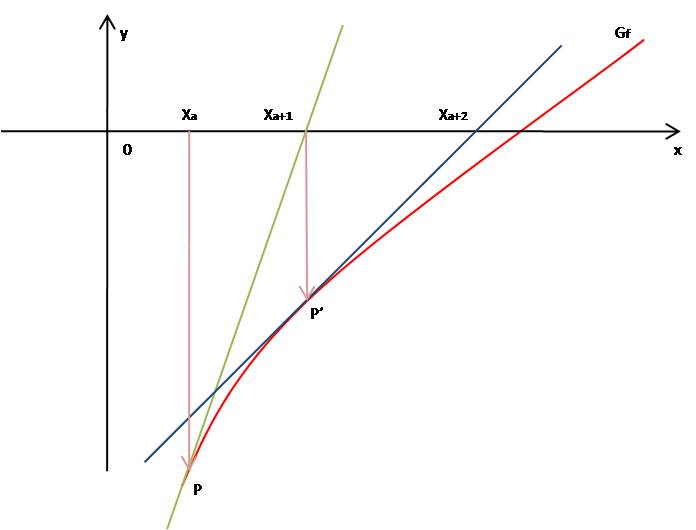
Beispiel: 

;

Für ist   ist , also liegt dazwischen eine Nullstelle, denn f ist stetig auf [1, 2].

      usw.