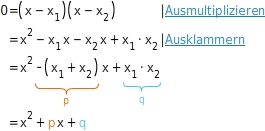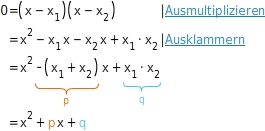Mit der p/q-Formel quadratische Gleichungen lösen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHerleitung der pq-Formel
Lösungsformel für eine quadratische Gleichung in Normalform
pq-Formel:
Die pq-Formel entsteht aus der
einer quadratischen Gleichung
durch
.
 für
:
für
:
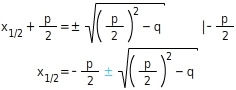
 für
:
für
:
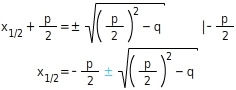
Lösen quadratischer Gleichungen
Lösungsformel für eine quadratische Gleichung in Normalform
pq-Formel:
Du setzt
und
in die pq-Formel ein:
 und
und
 und
und
Anzahl der Lösungen mit der Diskriminante bestimmen
Diskriminante D zur pq-Formel:
Betrachtest du die Diskriminante D der
, kannst du angeben, wie viele Lösungen eine
hat.
Ist D > 0, hat die Gleichung zwei Lösungen.
Ist D = 0, hat die Gleichung eine Lösung.
Ist D < 0, hat die Gleichung keine Lösung.
Satz von Vieta
Francois Viète (lat. Vieta) entdeckte den Zusammenhang zwischen p und q und den Lösungen
und
der quadratischen Gleichung
:
Du kannst mit dem Satz von Vieta überprüfen, ob zwei Werte Lösungen einer gegebenen quadratischen Gleichung sind. (
)
Sind
und
Lösungen der Gleichung
?
Du setzt
und
in die Gleichungen ein:
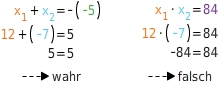 Daher ist mindestens einer der Werte keine Lösung der quadratischen Gleichung.
Du kannst den Satz von Vieta anwenden, um die Lösungen einer quadratischen Gleichung zu „erraten“.
Daher ist mindestens einer der Werte keine Lösung der quadratischen Gleichung.
Du kannst den Satz von Vieta anwenden, um die Lösungen einer quadratischen Gleichung zu „erraten“.
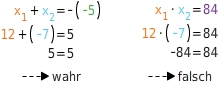 Daher ist mindestens einer der Werte keine Lösung der quadratischen Gleichung.
Du kannst den Satz von Vieta anwenden, um die Lösungen einer quadratischen Gleichung zu „erraten“.
Daher ist mindestens einer der Werte keine Lösung der quadratischen Gleichung.
Du kannst den Satz von Vieta anwenden, um die Lösungen einer quadratischen Gleichung zu „erraten“.
Welche Lösungen hat die Gleichung
?
Du setzt
für p und
für q in die Gleichungen ein und suchst nach Zahlen für
und
, die beide Gleichungen erfüllen:
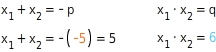 Die beiden Faktoren 2 und 3 von 6 sind Lösungen der quadratischen Gleichung. Du bestätigst das durch Einsetzen:
Die beiden Faktoren 2 und 3 von 6 sind Lösungen der quadratischen Gleichung. Du bestätigst das durch Einsetzen:
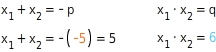 Die beiden Faktoren 2 und 3 von 6 sind Lösungen der quadratischen Gleichung. Du bestätigst das durch Einsetzen:
Die beiden Faktoren 2 und 3 von 6 sind Lösungen der quadratischen Gleichung. Du bestätigst das durch Einsetzen:
Herleitung des Satzes von Vieta
Für eine quadratische Gleichung in Normalform (
) gilt der Satz von Vieta:
und
.
Den
kannst du aus der
herleiten.
Wenn
und
die Lösungen der
sind, dann gilt: