+49 30 300 2440 00
 – Mo bis Fr von 8:30 - 17 Uhr

Maßstäbliches Vergrößern und Verkleinern

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, wie du eine Figur oder ein Objekt maßstäblich vergrößerst oder verkleinerst und wie du diese Vergrößerung oder Verkleinerung mit dem „Rücknahmefaktor“ wieder rückgängig machen kannst.

Maßstäbliches Vergrößern oder Verkleinern von Figuren

Wenn du eine Figur maßstäblich vergrößern oder verkleinern möchtest, multiplizierst du alle Seitenlängen der Figur mit demselben positiven Faktor k und lässt die Winkel gleich.
Mit einem Faktor k > 1 kannst du das Original vergrößern.Mit einem Faktor k < 1 kannst du das Original verkleinern.Für k = 1 sind beide Figuren kongruent.
Jeder Vergrößerungs- oder Verkleinerungsfaktor kann auch in Prozent angegeben werden. Dafür multiplizierst du den Faktor k mit 100.
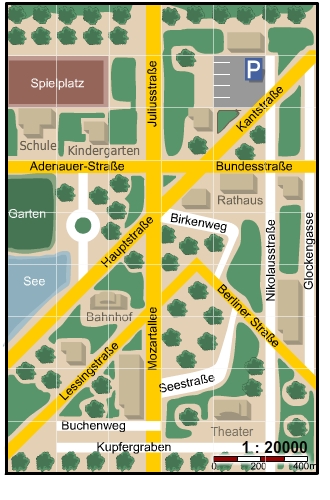
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_1.jpg
Ein Stadtplan ist eine maßstäbliche Verkleinerung einer vereinfachten Stadtansicht aus der Luft. Alle Gebäude und Straßen werden mit demselben Faktor verkleinert. Dieser Faktor ist als Maßstab auf den Plänen angegeben.
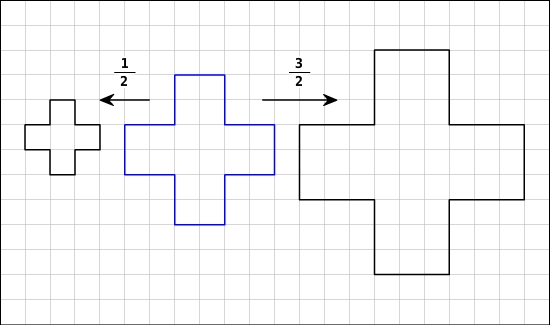
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_2.jpg
Die erste Figur ist eine Verkleinerung der blauen Originalfigur mit dem Faktor k 1 = 1 2 : 2 Kästchen · 1 2 = 1 Kästchen Die zweite Figur ist eine Vergrößerung der Originalfigur mit dem Faktor k 2 = 3 2 : 2 Kästchen · 3 2 = 3 Kästchen
Anna möchte eine Buchseite ( 11.5 cm x 18 cm ) vergrößern. Auf dem Kopierer wählt sie die Einstellung 141 % .Welche Abmessungen hat die Kopie der Buchseite?
Maße der Vergrößerung bestimmen
Die Vergrößerung auf 141 % entspricht dem Vergrößerungsfaktor k = 141 100 = 1.41 : 11.5 cm · 1.41 ≈ 16.2 cm   18 cm · 1.41 ≈ 25.4 cm
Maße der Buchseite nach der Vergrößerung: 16.2 cm x 25.4 cm
Paul möchte eine Doppelseite ( 38.8 cm x 26 cm ) aus einem Buch verkleinern. Auf dem Kopierer wählt er die Einstellung 60 % .Welche Abmessungen hat die Kopie der Doppelseite?
Maße der Verkleinerung bestimmen
Die Verkleinerung auf 60 % entspricht dem Verkleinerungsfaktor k = 60 100 = 0.6 : 38.8 cm · 0.6 ≈ 23.3 cm   26 cm · 0.6 = 15.6 cm
Maße der Buchseite nach der Verkleinerung: 23.3 cm x 15.6 cm

Maßstäbliches Vergrößern oder Verkleinern mit zwei Faktoren

Eine maßstäbliche Vergrößerung oder Verkleinerung kannst du auch in mehreren Schritten durchführen. Der Gesamtfaktor ist das Produkt der Faktoren der Einzelschritte.Du kannst somit die gesamte Vergrößerung oder Verkleinerung in einem Schritt mit dem errechneten Gesamtfaktor durchführen.
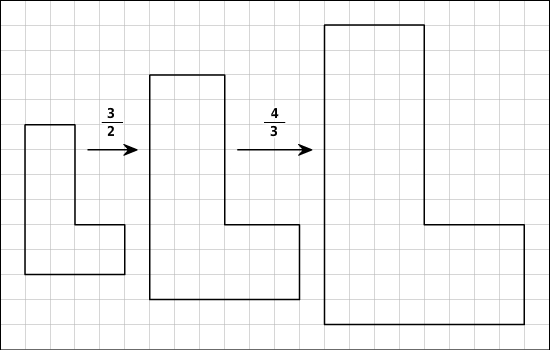
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_3.jpg
Die Figur wird im ersten Schritt mit dem Faktor k 1 = 3 2 und anschließend mit dem Faktor k 2 = 4 3 vergrößert. Insgesamt ergibt sich der Vergrößerungsfaktor k = k 1 · k 2 = 3 2 · 4 3 = 2 .
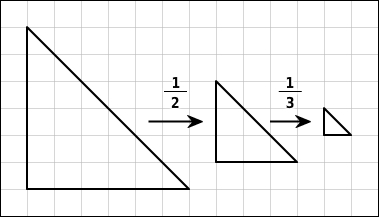
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_4.jpg
Die Figur wird im ersten Schritt mit dem Faktor k 1 = 1 2 und anschließend mit dem Faktor k 2 = 1 3 verkleinert. Insgesamt ergibt sich der Verkleinerungsfaktor k = k 1 · k 2 = 1 2 · 1 3 = 1 6 .

Rücknahmefaktor einer maßstäblichen Vergrößerung oder Verkleinerung

Mit dem Rücknahmefaktor kann eine maßstäbliche Vergrößerung oder Verkleinerung rückgängig gemacht werden.Wenn eine Figur mit einem Faktor k maßstäblich vergrößert oder verkleinert wird, dann ist jede Bildlänge der vergrößerten oder verkleinerten Figur das k -fache der entsprechenden Originallänge. Um diese Vergrößerung oder Verkleinerung rückgängig zu machen, suchst du die Zahl k' , für die mit der Seitenlänge a der Originalfigur gilt:
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_5.jpg
Der Rücknahmefaktor ist der Kehrwert des Faktors k, mit dem maßstäblich vergößert bzw. verkleinert wurde.
Rücknahmefaktor: k' = 1 k
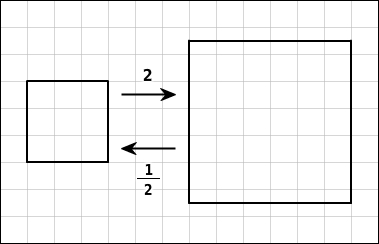
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_6.jpg
Um die Vergrößerung mit dem Faktor k' wieder rückgängig zu machen, muss 2 · k' = 1 gelten. Damit gilt für den Rücknahmefaktor k' = 1 2 .

änderung des Flächeninhaltes bei einer maßstäblichen Vergrößerung oder Verkleinerung

Bei einer Vergrößerung oder Verkleinerung einer Figur mit dem Faktor k vergrößert oder verkleinert sich der Flächeninhalt der Figur mit dem Faktor k 2 .
Bei einer maßstäblichen Vergrößerung des Rechtecks ABCD mit den Seitenlängen a = 2.3 cm und b = 5.8 cm entsteht das Rechteck A'B'C'D' mit dem Flächeninhalt A' = 53.36 cm 2 . Mit welchem Faktor k wurde das Rechteck ABCD vergrößert?
Faktor bestimmen
Den Flächeninhalt A' einer mit dem Faktor k maßstäblich vergrößerten Figur bestimmst du aus dem Flächeninhalt A der Originalfigur mit A' = A · k 2 . Das Rechteck ABCD hat den Flächeninhalt:
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_7.jpg
Den positiven Faktor k bestimmst du so:
/wp-content/uploads/media/kem_Geo3_Geo3VVAeVV_8.jpg
Damit ergibt sich der Vergrößerungsfaktor k = 2 .
Das Rechteck wurde mit dem Faktor k = 2 vergrößert.