Lösen von Exponentialgleichungen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenLösen durch Exponentenvergleich
Einfache
kannst du im Kopf lösen, wenn du auf beiden Seiten der Gleichung
mit derselben
hast. Manchmal ist das offensichtlich, manchmal benötigst du eine einfache Umformung.
Linke Seite vereinfachen:
Also:
Exponentenvergleich ergibt:
Also:
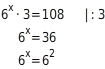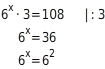Exponentenvergleich ergibt:
Du schreibst beide Seiten als Potenzen derselben Basis:
und
Exponentenvergleich ergibt:
Lösen durch Logarithmieren
Durch
erhältst du
und nach der
Du berechnest x mit dem Taschenrechner, indem du die Taste 
verwendest. Das Ergebnis rundest du auf zwei Stellen nach dem Komma:
≈
Du berechnest x mit dem Taschenrechner, indem du die Taste verwendest. Das Ergebnis rundest du auf zwei Stellen nach dem Komma:
≈
Logarithmieren und Anwendung der Exponentenregel:
Nach x umstellen:
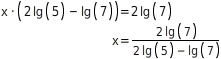Du berechnest x mit dem Taschenrechner, indem du die Taste 
verwendest:
(
)
Das Ergebnis rundest du auf zwei Stellen nach dem Komma:
≈
Nach x umstellen:
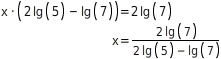Du berechnest x mit dem Taschenrechner, indem du die Taste verwendest:
(
)
Das Ergebnis rundest du auf zwei Stellen nach dem Komma:
≈
lässt sich nicht exakt lösen, sondern nur näherungsweise durch Einsetzen geeigneter Werte.
:
und
Lösung liegt zwischen 0 und 1.
:
≈
>
≈
Lösung liegt zwischen
und 1.
Ein guter
für x ist
.
Lösung liegt zwischen 0 und 1.
:
≈
>
≈
Lösung liegt zwischen
und 1.
Ein guter
für x ist
.
