Karten, Lagepläne und Maßstäbe kennenlernen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren„Hier erfährst du wie du Pläne, Karten und Umrisse lesen und verstehen und wie du Längen maßstabsgetreu berechnen kannst. “
Planquadrate in Karten
Karten oder Pläne werden häufig zur besseren übersicht in Planquadrate eingeteilt. Städte, Straßen, Flüsse, … kannst du auf der Karte anhand der Angabe eines Planquadrats in der Legende so schneller finden. Die Planquadrate werden meist mit Buchstaben und Ziffern beschriftet. So ist jedes Planquadrat eindeutig gekennzeichnet.
Das orange gefärbte Planquadrat wird mit B2 bezeichnet, weil es in der Zeile „B“ und in der Spalte „2“ steht.
Planquadrate in Karten
Diese Karte wurde in 10 x 10 Planquadrate eingeteilt. Die Zeilen wurden mit Buchstaben beschriftet, die Spalten mit Ziffern.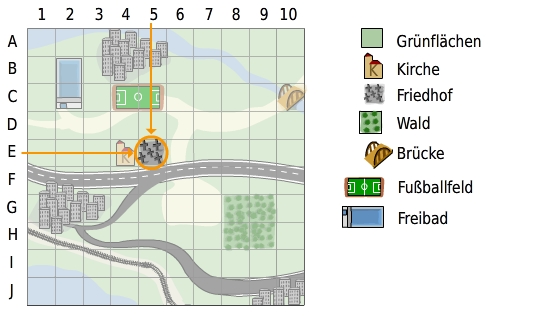
Verschiedene Orte können bestimmten Planquadraten zugeordnet werden.Zum Beispiel liegt der Friedhof im Planquadrat E5.
Der Maßstab
Bilder, Zeichnungen oder Karten stellen die Wirklichkeit verkleinert oder vergrößert dar. Der Maßstab beschreibt, wie stark verkleinert oder vergrößert wurde. Landkarten oder Grundrisse werden meist verkleinert dargestellt.Technische Zeichnungen oder auch Zeichnungen von Insekten (z.B. Ameise,…) werden häufig vergrößert dargestellt. Ein Maßstab wird über ein Verhältnis zweier Zahlen angegeben. - 1 : 10 bedeutet, dass
auf der Karte in Wirklichkeit
sind.- 1 : 100 bedeutet, dass
auf der Karte in Wirklichkeit
sind. Also
auf der Karte entspricht
in Wirklichkeit.- 1 : 100000 bedeutet, dass
auf der Karte in Wirklichkeit
sind.
sind
. Also
auf der Karte entspricht
in Wirklichkeit.
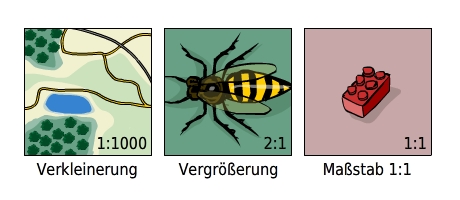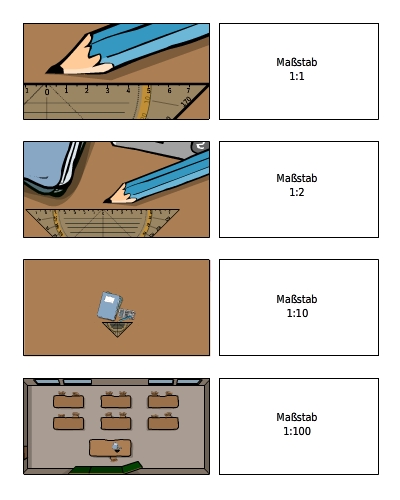
Je größer die zweite Zahl ist, umso kleiner ist der Maßstab.Je kleiner die zweite Zahl ist, umso größer ist der Maßstab.
Je größer die zweite Zahl ist, umso kleiner ist der Maßstab.Je kleiner die zweite Zahl ist, umso größer ist der Maßstab.
Berechnen der echten Größe
Der Maßstab 1 : 3 bedeutet, dass
auf der Karte
in Wirklichkeit sind.
Die Breite der Kerze wurde im Bild mit
dargestellt. Sie wurde im Maßstab 1 : 3 dargestellt. Du rechnest:
Die Kerze hat in Wirklichkeit eine Breite von
.
Die Schildkröte wurde im Maßstab 1 : 4 verkleinert dargestellt. Berechne die echte Länge der Schildkröte.
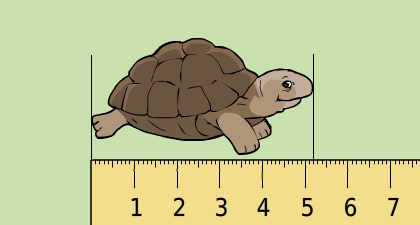
Maßstab berechnen
Die Schildkröte ist auf dem Bild
und
lang. Der Maßstab 1 : 4 bedeutet, dass
auf dem Bild
in Wirklichkeit sind. Ebenso entsprechen
auf der Karte
in Wirklichkeit.Du berechnest die Länge der Schildkröte in Wirklichkeit:
Die Schildkröte ist in Wirklichkeit
und
lang.
Die Maßstabsleiste
Auf vielen Karten und Abbildungen findet man nicht nur den Maßstab der Karte, sondern auch eine Maßstabsleiste. Auf der Maßstabsleiste ist der Maßstab mit den wirklichen Längen abgebildet. Die Maßstabsleiste hilft dir, Entfernungen auf der Karte abzumessen oder abschätzen zu können.
Maßstabsleiste in Maßstab umrechnen
Welcher Maßstab gehört zu dieser Maßstabsleiste?
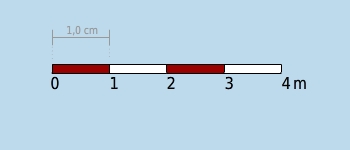
Maßstabsleiste kennenlernen
Die Maßstabsleiste ist in vier Teile eingeteilt.
ist
,
sind
,
sind
usw.
im Plan ist
in Wirklichkeit.
=
sind
das entspricht einem Maßstab von 1 : 100.
Der Maßstab beträgt 1 : 100.
Berechnen der echten Größe
Dies ist die Karte des Schulgeländes der Schule „Am Regenbogenteich“. Nick möchte wissen, welche Maße die Sporthalle hat. Er misst in einer Zeichnung mit einem Lineal: a =
b =
Gib die echte Länge und Breite der Sporthalle an.
Schulplan mit Maßstabsleiste:
Länge berechnen
Die Maßstabsleiste gibt an, dass
in der Karte
in Wirklichkeit entsprechen. Die Länge der Sporthalle beträgt in der Karte
. Echte Länge der Sporthalle:
Die Breite der Sporthalle beträgt in der Karte
.Echte Breite der Sporthalle:
Die Maße der Sporthalle betragen:a =
b =
Vergrößerung und Verkleinerung
Du kannst Zeichnungen oder Gegenstände vergrößert oder verkleinert zeichnen. Dies kannst du anhand eines Karorasters machen oder mit einer Maßstabsangabe.
Beim Karoraster vergrößerst oder verkleinerst du meist ohne genaue Maßangabe.
Mit dem Maßstab vergrößerst oder verkleinerst du auf eine bestimmte Größe.
Vergrößern mit einem Karoraster
Du möchtest ein Haus, das du in deinem Bastelbuch gefunden hast, vergrößern.
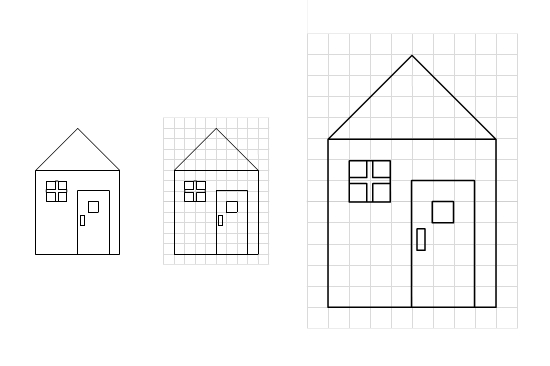
1) Du legst ein Karoraster über das Haus. 2) Du zeichnest ein neues Karoraster mit größeren Karos.3) Wichtige Eckpunkte des ersten Hauses überträgst du ins neue Raster (zum Beispiel die Ecken des Hauses oder den Giebel) 4) Du vervollständigst deine Zeichnung.
Verkleinern mit dem Karoraster
Du möchtest ein Haus, das du in deinem Bastelbuch gefunden hast, verkleinern.
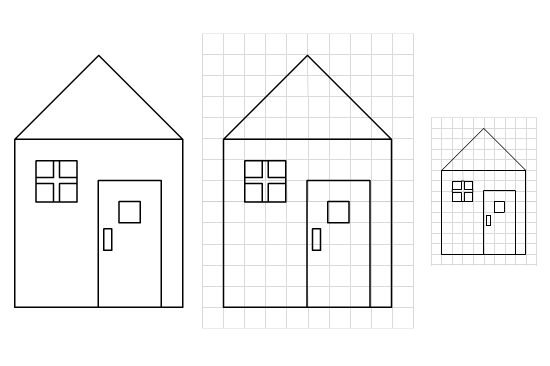
1) Du legst ein Karoraster über das Haus. 2) Du zeichnest ein neues Karoraster mit kleineren Karos.3) Wichtige Eckpunkte des ersten Hauses überträgst du ins neue Raster (zum Beispiel die Ecken des Hauses oder den Giebel) 4) Du vervollständigst deine Zeichnung.
Verkleinern mit einer Maßstabsangabe
Verkleinere die Zahl 2 im Maßstab 1 : 3.
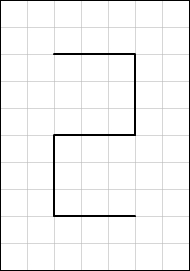
Mit Maßstab verkleinern
Da du im Maßstab 1 : 3 verkleinern sollst, teilst du alle Seitenlängen durch 3. 1 Kästchen in der neuen Zeichnung entsprechen 3 Kästchen in der alten Zeichnung.
Diese Zeichnung entspricht nun dem Maßstab 1 : 3 zur vorherigen Zeichnung.
