Höhensatz und Kathetensatz
Online Mathe üben mit bettermarks
- Über 2.400 Übungen mit fast 200.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Hier lernst du den Kathetensatz und den Höhensatz kennen. Diese beiden Sätze und der Satz des Pythagoras bilden zusammen die Satzgruppe des Pythagoras.
Der Kathetensatz des Euklid
In einem rechtwinkligen Dreieck teilt die Höhe auf der Hypotenuse diese in zwei Strecken, die Hypotenusenabschnitte p und q.
In einem rechtwinkligen Dreieck ABC mit rechtem Winkel im Punkt C und Hypotenusenabschnitten p und q gilt:
und
Flächeninhalte vergleichen
Der Flächeninhalt des Kathetenquadrats beträgt 36
6 · 6 = 36 .
Der Flächeninhalt des Rechtecks über dem Hypotenusenabschnitt p beträgt ebenfalls 36
4 · 9 = 36 .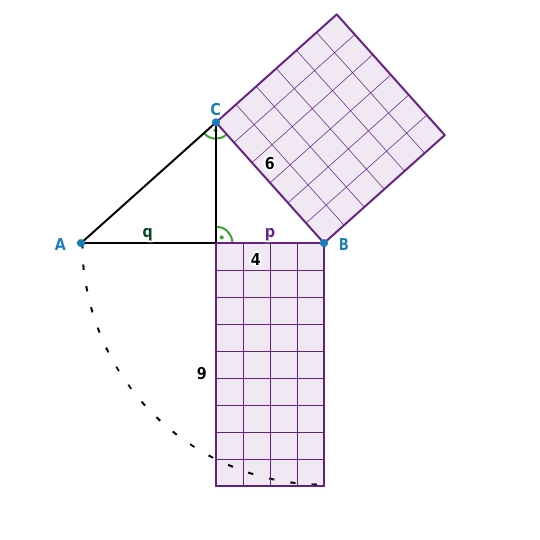
Mit Hilfe des Kathetensatzes kannst du die Längen in einem rechtwinkligen Dreieck berechnen.
Hypotenuseanabschnitt p
(Maße in cm)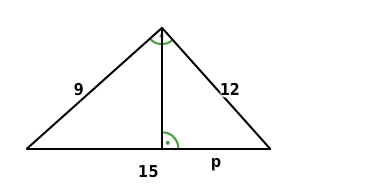
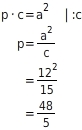
Länge des Hypotenusenabschnitts p (in cm):
Nach dem Kathetensatz gilt
Du stellst nach p um und setzt 12 für a und 15 für c ein.
Länge des Hypotenusenabschnitts p (in cm):
Nach dem Kathetensatz gilt
Du stellst nach p um und setzt 12 für a und 15 für c ein.
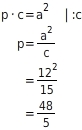
Kathete b
(Maße in cm)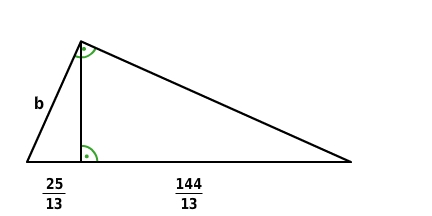
Länge der Kathete b (in cm):Nach dem Kathetensatz gilt:
c ist die Hypotenuse. Du addierst die Hypotenusenabschnitte.
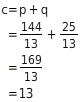Du setzt 13 für c und
für q in den Kathetensatz ein und ziehst die Wurzel.
Also :
Länge der Kathete b (in cm):Nach dem Kathetensatz gilt:
c ist die Hypotenuse. Du addierst die Hypotenusenabschnitte.
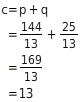Du setzt 13 für c und
für q in den Kathetensatz ein und ziehst die Wurzel.
Also :
Der Höhensatz des Euklid
In einem rechtwinkligen Dreieck teilt die Höhe auf der Hypotenuse diese in zwei Strecken, die Hypotenusenabschnitte p und q.
In einem rechtwinkligen Dreieck mit Hypotenusenabschnitten p und q und Höhe h gilt:
Flächeninhalte vergleichen
Der Flächeninhalt des Höhenquadrats beträgt 16
4 · 4 = 16 .
Der Flächeninhalt des Rechtecks über dem Hypotenusenabschnitt p beträgt ebenfalls 16
2 · 8 = 16 .
Mit Hilfe des Höhensatzes kannst du die Längen in einem rechtwinkligen Dreieck berechnen.
Hypotenusenabschnitt q
Maße (in cm)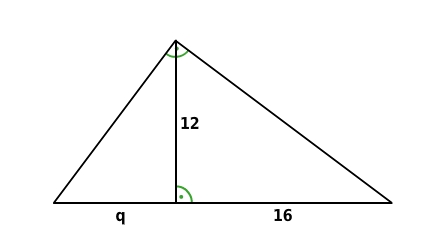
Länge des Hypotenusenabschnitts q (in cm):
Nach dem Höhensatz gilt:
Du stellst nach q um und setzt 12 für h und 16 für p ein.
Länge des Hypotenusenabschnitts q (in cm):
Nach dem Höhensatz gilt:
Du stellst nach q um und setzt 12 für h und 16 für p ein.