Funktionsgleichung bestimmen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du Funktionsgleichungen zu linearen Funktionen aufstellen kannst.
Funktionsgleichungen aufstellen durch Ablesen am Graphen
Der Graph einer linearen Funktion ist eine Gerade. Die Gleichung hat die Form . Dabei bezeichnet den Wert für die Steigung und den -Achsenabschnitt. Hast du von einer linearen Funktion den Graphen, also die Gerade gegeben, kannst du beide Werte direkt der graphischen Darstellung entnehmen.
Bestimme zum abgebildeten Graphen die Funktionsgleichung.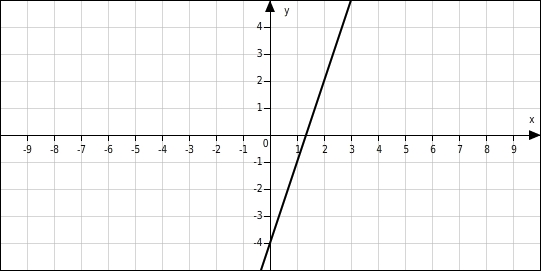 
Gleichung aufstellen
Die Gerade schneidet die y-Achse an der Stelle -4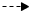 
Am Steigungsdreieck kannst du ablesen, dass die Gerade die Steigung hat.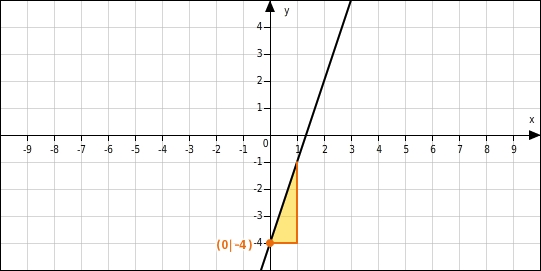 
Bestimme zum abgebildeten Graphen die Funktionsgleichung.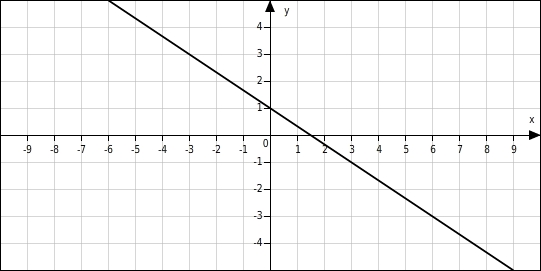 
Gleichung aufstellen
Die Gerade schneidet die y-Achse an der Stelle 1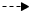 
Am Steigungsdreieck kannst du ablesen, dass die Gerade hat die Steigung hat.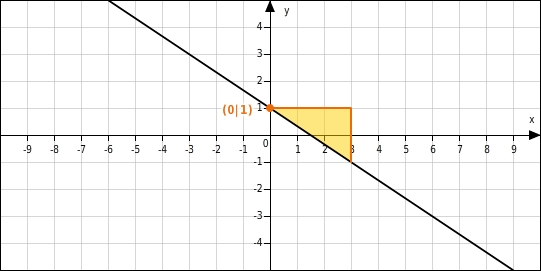 
Funktionsgleichungen aufstellen zur Berechnung besonderer Punkte
Viele Zusammenhänge in Natur und Technik lassen sich durch lineare Funktionen beschreiben. Oft haben die besonderen Punkte der Graphen (Nullstelle, y-Achsenabschnitt, Schnittpunkte mit anderen Graphen) in diesen Beispielen auch eine besondere Bedeutung.
In einer Region ist eine bestimmte Pflanzenart an einem Virus erkrankt. Der Prozentsatz der kranken Pflanzen wird alle 5 Jahre erfasst und registriert. Eine lineare Funktion beschreibt den Trend recht gut, der Anteil der kranken Pflanzen nimmt ab, die Pflanzen werden immun gegen den Virus. Bei der ersten Zählung werden der Pflanzen als krank gezählt. Welcher Anteil der Pflanzen wird nach 70 Jahren noch krank sein? Wann wird es voraussichtlich in dieser Region erstmalig keine kranken Pflanzen mehr geben? 
Die Steigung der Geraden ermittelst du mit Hilfe eines Steigungsdreiecks: Die Gerade schneidet die y-Achse an der Stelle . Bei der ersten Zählung waren aller Pflanzen erkrankt.
Funktionsgleichung aufstellen
Funktionswert berechnen
Du setzt den Wert 70 für x in die Funktionsgleichung ein und berechnest y.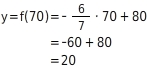 
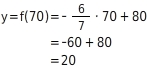
Nullstelle berechnen
Der berechnete Zeitpunkt, zu dem voraussichtlich keine kranken Pflanzen mehr gezählt werden, entspricht der Nullstelle der Funktion. Du berechnest die Nullstelle (f(x) = 0) indem du 0 für y in die Funktionsgleichung einsetzt und die Gleichung nach x auflöst.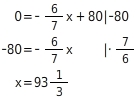 
Da die Zählung alle 5 Jahre stattfindet, wird man voraussichtlich erstmalig bei der Zählung nach 95 Jahren keine kranken Pflanzen mehr finden.
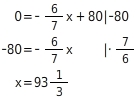
Funktionsgleichungen mit Punkt und Steigung bestimmen
Hast du von der Funktion die Steigung und einen Punkt des Graphen gegeben, kannst du den y-Achsenabschnitt rechnerisch bestimmen.
Der Graph einer linearen Funktion f verläuft durch den Punkt P( | ) und hat die Steigung . Bestimme die Funktionsgleichung von f. Der Punkt Q( |y) liege ebenfalls auf dem Graphen der Funktion. Bestimme die y-Koordinate. Q( | )
Funktionsgleichung angeben
Der Punkt P( | ) liegt auf der Geraden. Also erfüllen seine Koordinaten die zugehörige Funktionsgleichung. Die Funktionsgleichung hat die Form Du bestimmst den y-Achsenabschnitt b, indem du die Koordinaten des Punktes P in die Funktionsgleichung einsetzt und die Gleichung nach b auflöst: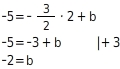 
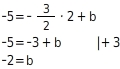
y-Koordinate des Punktes Q bestimmen
Du setzt die x-Koordinate des Punktes Q in die Funktionsgleichung ein und berechnest y.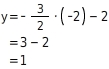 
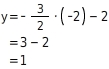
Funktionsgleichungen mit Hilfe von zwei Punkten bestimmen
Hast du von der Funktion zwei Punkte P und Q des Graphen gegeben, kannst du die Steigung mit Hilfe der Steigungsformel rechnerisch bestimmen. Mit Hilfe der Funktionsgleichung kannst du dann überprüfen, ob ein beliebiger weiterer Punkt auch auf dem Graphen der Funktion liegt.
Bestimme die Funktionsgleichung zur Geraden, die durch die Punkte P( | ) und Q( | ) verläuft. überprüfe, ob die Punkte R( | ) und S( | ) auf der Geraden liegen.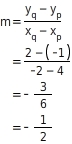 
Steigung mit Hilfe der Steigungsformel berechnen
Du setzt die Koordinaten der Punkte P und Q in die Steigungsformel ein und berechnest die Steigung.
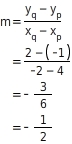
y-Achsenabschnitt bestimmen und Funktionsgleichung angeben
Du setzt die Koordinaten eines der beiden Punkte in die Funktionsgleichung ein und löst die Gleichung nach b auf. Mit P( | ) gilt: 
Zugehörigkeit des Punktes R überprüfen
Du setzt die Koordinaten des Punktes R in die Funktionsgleichung ein und überprüfst, ob eine wahre Aussage entsteht.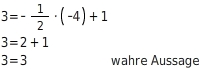 
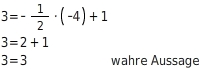
Der Punkt R( | ) liegt auf der Geraden.
Zugehörigkeit des Punktes S überprüfen
Du setzt die Koordinaten des Punktes S in die Funktionsgleichung ein und überprüfst, ob eine wahre Aussage entsteht. 
Der Punkt S( | ) liegt nicht auf der Geraden.
